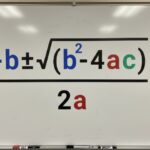Share Post:
Patterns are what make mathematics feel alive. They give structure to numbers, shapes, and ideas, showing how one thing connects to another in ways that repeat or make sense. When you notice something that happens again and again, or a rule that keeps working no matter how far you go, you are looking at a pattern.
It might be a simple sequence of numbers like 2, 4, 6, 8, 10. Or a hexagon grid that covers a surface perfectly, like the honeycomb in a beehive. Or a line on a chart that climbs steadily upward even when the dots scatter a bit. Patterns let us predict, describe, and simplify. They turn scattered facts into structure.
Below is a complete, practical guide to what counts as a pattern in math, why patterns matter, and how to work with them in arithmetic, geometry, and data.
Table of Contents
ToggleA Simple Definition
A pattern in mathematics is a regularity that can be described by a rule. The rule might involve numbers, geometric shapes, functions, or statistical trends. Britannica calls mathematics “the science of structure, order, and relation,” and that definition makes pattern spotting a central part of the subject.
In classrooms, a common way to define it is: an ordered set of numbers, shapes, or objects arranged according to a rule. It’s a friendly way to introduce students to the idea that math is built on repetition and order.
Patterns help people make sense of math because they show how things are connected. Instead of memorizing isolated facts, you start to see why something works again and again.
Why Patterns Matter in Math Learning
Every math curriculum highlights patterns as part of reasoning. They are not just a topic to learn, but a habit of thinking. Two “Mathematical Practice Standards” describe it clearly:
MP7: Look for and Make Use of Structure.
Students notice repeated structure inside expressions or diagrams and use it to reason faster.
Example: 7 × 8 can be seen as 7 × (5 + 3). That pattern prepares learners for distributive reasoning.
MP8: Look for and Express Regularity in Repeated Reasoning.
When a process repeats, you search for a shortcut and write a general rule.
Education researchers often say that patterning builds the foundation for algebra. When students describe how a pattern grows, they are already working toward expressing general rules with variables. State-level teaching standards also show how pattern awareness grows from spotting simple color or shape repeats in early grades to using formal algebraic notation and proofs in high school.
The Major Types of Mathematical Patterns
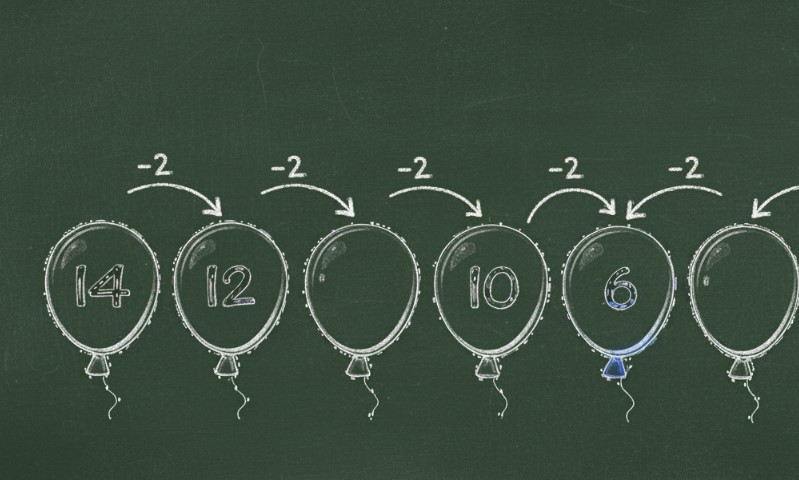
Mathematical patterns come in many forms, each revealing a different kind of structure. From repeating numbers to geometric shapes and data trends, every type follows its own rule but serves the same purpose: to show how order appears within variety.
1. Number Patterns and Sequences
Number patterns and sequences show how math captures repetition in the simplest form. They reveal how numbers grow, shrink, or repeat according to a clear rule, making it possible to predict what comes next with just a few starting terms.
Arithmetic Sequences
Each term changes by a constant difference.
- Formula: aₙ = a₁ + (n – 1) * d
- Example: 3, 6, 9, 12, 15. The difference d is 3.
These show steady, additive change, like saving the same amount each month.
Geometric Sequences
Each term changes by a constant factor.
- Formula: aₙ = a₁ * r^(n – 1)
- Example: 2, 4, 8, 16, 32. The ratio r is 2.
These describe multiplicative growth or decay, like population growth or compound interest.
Recursive Rules
Each term depends on the previous ones.
The Fibonacci sequence starts with 1, 1, and then each new term is the sum of the two before it:
Fₙ = Fₙ₋₁ + Fₙ₋₂ for n ≥ 3
Fibonacci numbers appear everywhere, from ancient math texts to the spiral of sunflower seeds.
Where Mathematicians Track Numeric Patterns
The On-Line Encyclopedia of Integer Sequences (OEIS) collects hundreds of thousands of numeric patterns used by researchers, teachers, and puzzle enthusiasts.
Why Number Patterns Matter
Recognizing the rule helps compute large terms quickly and identify what kind of behavior the sequence represents.
- Constant first differences indicate linear patterns.
- Constant ratios indicate exponential behavior.
Those clues form the foundation of algebraic thinking.
2. Functional Patterns
Functions describe how one quantity changes in relation to another. Patterns are the key to seeing what type of function you have.
Linear Patterns
Equal steps in x produce equal changes in y.
- Rule: y = m * x + b
The graph forms a straight line. This type of relationship shows steady, predictable change.
QuadraticPatterns
The second differences are constant.
- Rule: y = a * x² + b * x + c
You see this in motion problems, projectile paths, or growth that curves upward or downward.
Exponential Patterns
Equal steps in x multiply y by the same factor.
- Rule: y = a * b^x
That pattern signals compounding, like interest rates or bacterial growth.
MP8 (regularity in repeated reasoning) often comes into play here. When students calculate slopes several times and notice the pattern (change in y) / (change in x) , they end up creating the general rule for the slope of a line.
3. Geometric Patterns
Geometry gives us some of the most visually satisfying patterns.
Symmetry
A shape is symmetric if it can be flipped, turned, or shifted so that it maps onto itself.
Symmetry includes:
- Reflection (mirror symmetry)
- Rotation (turning around a point)
- Translation (sliding along a direction)
- Glide reflection (a slide combined with a flip)
In advanced terms, symmetry means a shape is invariant under certain transformations.
Tessellations
A tessellation is a pattern of shapes that covers a surface without gaps or overlaps.
Examples include:
- Squares or triangles tiling a floor.
- Regular hexagons in a honeycomb.
Wallpaper Groups
When you classify repeating patterns on a plane by their symmetries, you find exactly 17 possible types.
These are known as the 17 wallpaper groups. Mathematicians like David E. Joyce have created helpful visual catalogs that show each one with clear diagrams.
Fractals and Self-Similarity
Some geometric patterns repeat at smaller and smaller scales. Think of the branching of trees or the outline of coastlines.
A fractal looks similar no matter how much you zoom in. Fractals have a fractional dimension , a way to measure how much space they fill.
Geometry in Art
The artist M. C. Escher turned mathematical patterning into visual magic. His interlocking birds, fish, and lizards fill the plane perfectly, offering a playful way to explore tessellations and symmetry.
4. Statistical and Data Patterns
Patterns also live in data. They are the signal inside the noise.
Trends and Рelationships
Scatter plots show how one variable changes with another.
- A straight-line trend means a linear relationship.
- A curve might suggest a quadratic or exponential link.
- A cloud with no clear shape likely has no strong relationship.
If the spread of points grows with the input, that is called heteroscedasticity . The NIST Engineering Statistics Handbook explains this and other useful diagnostics.
Residual Patterns
After fitting a model, statisticians inspect the residuals (the differences between predictions and actual values).
- If the residuals look random and evenly spread around zero, the model fits well.
- If they show curves or a changing spread, the model missed a pattern.
Autocorrelation and Time Series
When data comes from time sequences, nearby points may be related.
- Strong correlation between consecutive values suggests a time pattern.
- If the correlation slowly fades, an autoregressive model might fit.
- If correlations are near zero, the sequence is likely random.
Healthy Skepticism
Pattern recognition is powerful, but it can trick you. Small samples can fake structure, and overly flexible models can find patterns that are not real.
Statisticians use visual checks, cross-validation, and test sets to make sure a detected pattern truly generalizes.
How to Detect and Describe Patterns
Numbers and Algebra
Numbers and algebra are where most people first start spotting patterns. You notice how certain calculations repeat, how sequences grow, and how those repetitions can be written as simple rules. It’s the part of math where structure turns into a formula.
1. Check first differences or ratios
- Constant first difference → linear growth
- Constant ratio → exponential growth
2. Build an input-output table
Write down the inputs and outputs.
- Equal steps in input produce equal adds in output → linear rule y = m * x + b
- Equal steps multiply the output → exponential rule y = a * b^x
3. Use recursion, then generalize
Start with a next-term rule.
Compute several terms.
Find a general formula like
aₙ = a₁ + (n – 1) * d or aₙ = a₁ * r^(n – 1)
4. Look for Structure in Expressions
- Factor x² + 9x + 14 by seeing that 14 = 2 * 7 and 9 = 2 + 7.
- Rewrite 7 * 8 as 7 * (5 + 3) to highlight structure, preparing for distributive reasoning.
Geometry
Geometry is where patterns turn visual. Shapes repeat, reflect, and fit together in ways that reveal balance and structure. It’s math you can actually see.
1. Test for symmetry types
- Reflection, rotation, translation, or glide reflection
- Identify axes or centers when they exist
2. Identify tessellations
- Does the pattern cover the plane with no gaps or overlaps?
- If yes, classify which wallpaper group it might belong to.
3. Notice self-similarity
- If zooming reveals the same motif, it’s likely a fractal.
- Fractal dimension describes how its detail grows with scale.
Data and Statistics
Patterns in data show where the numbers are trying to tell a story. In statistics, you look for structure hidden inside variation: trends, clusters, or repeating behaviors that reveal how things are connected or changing over time.
1. Plot first
- Use scatter plots or time series charts to spot structure visually.
2. Inspect residuals
- Random residuals mean the model works well.
- Curves or trends suggest missing structure.
3. Check autocorrelation
- Flat autocorrelation → no time-based pattern.
- Slowly decaying autocorrelation → autoregressive structure.
4. Validate assumptions
- Good residuals hover near zero with constant spread.
- Use NIST’s visual galleries to compare examples.
Classroom-Ready Ways to Build Pattern Skills

Building pattern skills in the classroom starts with curiosity. When students explore how numbers or shapes repeat and grow, they begin to see the logic behind math instead of just memorizing it.
A few simple activities can turn that spark of curiosity into genuine mathematical thinking.
Early Grades
Using tiles or blocks to build growing patterns helps children connect arithmetic and algebra. Teachers often ask:
- What comes next?
- How many at step ten?
- Can you write a rule for step n ?
Research from NCTM (National Council of Teachers of Mathematics) shows how such hands-on patterning helps students generalize and reason symbolically.
Middle School
Programs like NRICH (University of Cambridge) design activities where students look at several cases and then describe a rule that always works. That shift from examples to general statements is a key milestone toward formal proofs.
Geometry Through Art
Escher-inspired tessellation projects or “symmetry hunts” in architecture help students connect design, geometry, and algebraic thinking in a way that feels real and creative.
Quick Reference Table
| Pattern Family | Typical Signal | Rule in WordPress-Friendly Format | What It Predicts |
| Arithmetic sequence | Constant first difference | aₙ = a₁ + (n – 1) * d | Linear growth |
| Geometric sequence | Constant ratio | aₙ = a₁ * r^(n – 1) | Exponential growth or decay |
| Recursive sequence | Depends on previous terms | Fₙ = Fₙ₋₁ + Fₙ₋₂ | Efficient generation and general formulas |
| Linear function | Equal input steps add outputs equally | y = m * x + b | Straight lines and proportional change |
| Quadratic function | Constant second difference | y = a * x² + b * x + c | Parabolic motion or growth |
| Exponential function | Equal input steps multiply outputs | y = a * b^x | Compound growth or decay |
| Symmetry | Shape maps onto itself | Reflection, rotation, translation | Classification of shapes |
| Tessellation | No gaps or overlaps | Regular or semi-regular tiling | Efficient surface coverage |
| Wallpaper group | Repeating planar pattern | One of 17 symmetry types | Complete symmetry classification |
| Fractal | Self-similarity | Described by fractal dimension | Scaling and complexity |
| Data trend | Visible direction in points | Regression line or curve | Prediction |
| Autocorrelation | Lagged dependence | Autocorrelation plot, AR models | Time-series forecasting |
How to Write About a Pattern Precisely
Writing about a pattern clearly means showing what repeats and why it matters. A good explanation connects examples, rules, and reasoning so anyone can see the structure without guessing.
1. Name inputs and outputs.
Example: let n be the step number, and P(n) be the number of tiles.
2. Show small cases.
List the first few terms or shapes so readers can see the regularity.
3. State the rule.
For a growing “L” shape made of tiles, you might find P(n) = 4 * n + 1.
4. Justify the rule.
Explain with a drawing or count why it works for all n.
5. Check edge cases.
Make sure your rule fits even at n = 1.
6. Connect multiple views.
Link tables, graphs, and context. These habits align directly with MP7 and MP8.
Famous Mathematical Patterns

- Even, odd, and prime numbers: All follow clear rules that define special sets of integers.
- Pythagorean triples: Sets like (3, 4, 5) or (5, 12, 13) satisfy a² + b² = c² , revealing number structure with geometric meaning.
- Fibonacci in nature: Spiral counts in pinecones, sunflowers, and shells often match Fibonacci numbers. Britannica and many math education sites show the connection between nature’s growth patterns and numerical ratios.
Bringing It All Together
So what is a pattern in math? It is repetition that follows a reason. When you can name the reason, describe the rule, and confirm that it holds, you are doing mathematics at its core.
A clean line on a graph, a repeating tile floor, or the structure in a set of data all tell the same story. You notice something consistent, describe it, and use it to predict what comes next. That is what gives mathematics its power: it turns repetition into understanding, and structure into insight.
Whether you are helping children spot color patterns in tiles, analyzing symmetry in architecture, or checking correlations in a dataset, the process is the same. Look for regularity, describe it clearly, test it, and explain why it works.
Once you see patterns everywhere, you start to see mathematics not as a collection of formulas, but as the language of structure itself.
Related Posts:
- How can I make my 3rd-grade math fun? From Bored to Board!
- Who Invented Math: History, Facts and Table of Numerals
- What Are the Acronyms Used in Math? - A Beginner's Guide
- 14 Best Cool Math Games For Any Age
- Complete Guide to Teaching Math with Base 10 Blocks…
- Why Is Math So Hard? Exploring Common Challenges