As you venture into the world of mathematics, you’ll often encounter a series of acronyms. Think of them as shorthand notes, each containing a world of concepts and ideas within a few letters.
These are not just for convenience; they encapsulate some of the most profound ideas in math, giving you a shortcut to understanding complex theories and concepts. In this blog post, we will unearth the meaning and significance of thirty such acronyms. Let’s embark on this exciting journey!
1. BODMAS/BIDMAS/PEDMAS (Order of Operations)
The order of operations in mathematics determines the sequence in which operations are performed in an expression. In English-speaking countries, the acronyms BODMAS, BIDMAS, and PEDMAS are popular.
BODMAS
The BODMAS rule establishes that in a mathematical expression, operations enclosed in brackets are performed first, followed by orders (i.e., powers and roots), then division and multiplication (from left to right), and finally, addition and subtraction (from left to right).
BIDMAS/PEDMAS
BIDMAS and PEDMAS rules are variants of the BODMAS rule. They replace ‘orders’ with ‘indices’ or ‘exponents’, but the principle remains the same.
2. LCM and HCF/GCD (Number Theory)
In number theory, two critical acronyms that are commonly used are LCM (Least Common Multiple) and HCF or GCD (Highest Common Factor or Greatest Common Divisor).
LCM (Least Common Multiple)
The LCM of two or more integers is the smallest integer that is evenly divisible by each of the integers. The LCM can be found for any number of integers, and it plays a critical role in solving problems involving repetitions or cycles.
HCF/GCD (Highest Common Factor/Greatest Common Divisor)
The HCF or GCD of two or more integers is the largest number that divides each of the numbers without leaving a remainder. It is a fundamental concept in number theory and is used extensively in algebra.
3. PEMDAS (Calculus)
Calculus, the branch of mathematics dealing with rates of change and accumulation of quantities, uses the acronym PEMDAS.
PEMDAS
PEMDAS, similar to BODMAS/BIDMAS/PEDMAS, is another rule governing the order of operations. The PEMDAS rule asserts that operations in parentheses are carried out first, then exponents, followed by multiplication and division (from left to right), and lastly, addition and subtraction (from left to right).
Derivatives and Integrals (DX, DY, ∫)
In calculus, derivatives, and integrals are denoted by the acronyms DX and DY, and the symbol ∫, respectively. DX and DY represent infinitesimal changes in the variables x and y. ∫ symbolizes the integral sign, indicating integration or the computation of the area under a curve.
4. RHS and LHS (Algebra)
In algebra, two essential acronyms that you will frequently encounter are RHS and LHS, representing the two sides of an equation.
RHS (Right Hand Side)
In an equation, the term on the right side of the equals sign is known as the RHS. It signifies the output or result of the operations performed on the variables.
LHS (Left Hand Side)
Conversely, the term on the left side of the equals sign is known as the LHS. It represents the expression or the operations that need to be performed on the variables.
5. SOHCAHTOA (Trigonometry)
In trigonometry, the acronym SOHCAHTOA is an essential mnemonic that represents the fundamental relationships between the sides of a right triangle and the trigonometric ratios.
SOH (Sine equals Opposite over Hypotenuse)
SOH stands for Sine equals Opposite over Hypotenuse. It defines the ratio of the length of the side that is opposite to the angle to the length of the longest side of the triangle (hypotenuse).
CAH (Cosine equals Adjacent over Hypotenuse)
CAH stands for Cosine equals Adjacent over Hypotenuse. It represents the ratio of the length of the side next to the angle to the length of the hypotenuse.
TOA (Tangent equals Opposite over Adjacent)
TOA stands for Tangent equals Opposite over Adjacent. It represents the ratio of the length of the side opposite to the angle to the length of the side next to the angle.
6. DMS (Angle Measurement)
In geometry, the acronym DMS is used to denote a method of measuring angles. DMS stands for Degrees, Minutes, and Seconds, which are traditional units of measuring angles.
Degrees (D)
Degrees are the primary unit for measuring angles in the DMS system. A complete circle is divided into 360 degrees, and a right angle measures 90 degrees.
Minutes and Seconds (M and S)
In the DMS system, each degree is subdivided into 60 minutes, and each minute is further divided into 60 seconds. This system allows for precise measurements of angles.
7. FOIL (Algebra)
In algebra, the acronym FOIL is used as a mnemonic to remember the steps to multiply two binomials.
FOIL (First, Outer, Inner, Last)
The FOIL method stands for First, Outer, Inner, and Last. It means that the first terms of each binomial are multiplied together, then the outer terms, followed by the inner terms, and finally, the last terms of each binomial.
8. AAA, SAS, SSS (Geometry)
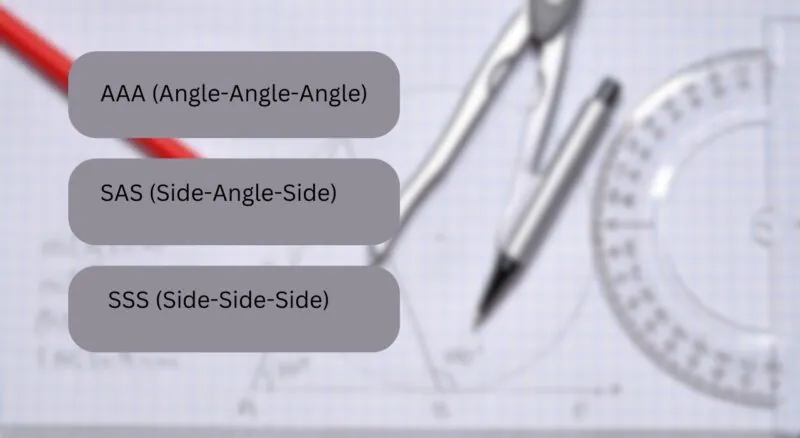
In geometry, especially when dealing with triangles, the acronyms AAA, SAS, and SSS are often used to refer to the conditions that can determine similarity or congruence between two triangles.
AAA (Angle-Angle-Angle)
AAA is a criterion for the similarity of two triangles, meaning if the corresponding angles of two triangles are equal, the triangles are similar.
SAS (Side-Angle-Side) and SSS (Side-Side-Side)
SAS and SSS are criteria for the congruence of two triangles. SAS states that if two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, the triangles are congruent. SSS states that if the three sides of one triangle are equal to the three sides of another triangle, the triangles are congruent.
9. CPCTC (Geometry)
In geometry, the acronym CPCTC is used to denote a property of congruent triangles.
CPCTC (Corresponding Parts of Congruent Triangles are Congruent)
CPCTC stands for Corresponding Parts of Congruent Triangles are Congruent. It is a fundamental property of congruent triangles stating that if two triangles are congruent, then their corresponding parts (sides and angles) are also congruent.
10. PEM (Statistics)
In Statistics, the acronym PEM is used to denote a method for calculating the mean of a data set.
PEM (Point Estimate of the Mean)
PEM stands for Point Estimate of the Mean. It refers to the method of using the sample mean as the point estimate of the population mean.
11. ACF and PACF (Statistics)
In time series analysis, which is a part of statistics, two essential acronyms are ACF and PACF.
ACF (Autocorrelation Function)
ACF stands for Autocorrelation Function. It’s a tool for identifying repeating patterns in a data set. It quantifies the correlation between observations in a time series and the corresponding observations from previous periods.
PACF (Partial Autocorrelation Function)
PACF, or Partial Autocorrelation Function, measures the correlation between observations at two points in time while controlling for any correlations due to the terms at intervening time points.
12. QED (Mathematical Proofs)
In the world of mathematical proofs, QED is a common term used to denote the end of a proof.
QED (Quod Erat Demonstrandum)
QED stands for Quod Erat Demonstrandum, a Latin phrase that translates to “what was to be demonstrated.” It’s traditionally placed at the end of a mathematical proof to indicate that the proof is complete.
13. PDF and CDF (Statistics)
When dealing with probability distributions in statistics, two key acronyms are PDF and CDF.
PDF (Probability Density Function)
PDF stands for Probability Density Function. For continuous random variables, the PDF is the function that describes the likelihood of different outcomes.
CDF (Cumulative Distribution Function)
CDF, or Cumulative Distribution Function, describes the cumulative probability that a random variable is less than or equal to a certain value.
14. LHS and RHS (Differential Equations)
In differential equations, similar to algebra, you will find the use of the acronyms LHS and RHS.
LHS (Left Hand Side)
In a differential equation, the term on the left side of the equals sign is called the LHS. It typically represents the derivative or the rate of change of a quantity.
RHS (Right Hand Side)
The RHS, or Right Hand Side, of a differential equation, usually represents the forcing function or the external input to the system.
15. IID (Statistics)
In statistics, IID is an acronym that defines a specific condition for a collection of random variables.
IID (Independent and Identically Distributed)
IID stands for Independent and Identically Distributed. It’s a term used to describe a collection of random variables that have the same probability distribution and are mutually independent.
16. RREF (Linear Algebra)
In the field of linear algebra, the acronym RREF is used to denote a specific form of a matrix.
RREF (Row-Reduced Echelon Form)
RREF stands for Row-Reduced Echelon Form. It’s a form of a matrix in which the leading entry of each row is 1, all elements in the column below and above the leading entry are 0, and each leading entry is to the right of the leading entry of the row above it.
17. WLOG (Mathematical Proofs)
In mathematical proofs, WLOG is a frequently used acronym.
WLOG (Without Loss of Generality)
WLOG stands for Without Loss of Generality. It is a phrase used to indicate that a statement or proof can be generalized without affecting the overall argument or result.
18. OLS (Statistics)
In statistics, OLS is a common method used in linear regression analysis.
OLS (Ordinary Least Squares)
OLS stands for Ordinary Least Squares. It’s a method used in linear regression to estimate the parameters of the regression line by minimizing the sum of the squares of the differences between the observed and predicted values.
19. NLP (Optimization)
In the field of optimization, NLP refers to a class of problems.
NLP (Nonlinear Programming)
NLP stands for Nonlinear Programming, which is a method used to solve optimization problems where the objective function or the constraints or both are nonlinear.
20. SVM (Machine Learning)
In machine learning, SVM is a commonly used algorithm for classification and regression analysis.
SVM (Support Vector Machine)
SVM stands for Support Vector Machine. It’s a supervised machine learning algorithm used for classification or regression analysis. It creates a hyperplane or set of hyperplanes in a high-dimensional space, which can be used for classification, regression, or other tasks.
Final Words
I hope this blog post has served as a helpful guide to the wide range of acronyms used in different fields of mathematics. The beauty of mathematics is that it is a universal language, one that can express complex ideas and abstract concepts in a simple and elegant manner.
The use of acronyms is just one example of how this language has been simplified and made more accessible for all to understand. Remember, these are just the tip of the iceberg; there are many more mathematical acronyms waiting to be discovered!
