Share Post:
In mathematics, accuracy in calculations is essential. To achieve this, specific rules guide us through the correct order of operations.
These rules are encapsulated in the mathematical acronyms BODMAS, BIDMAS, and PEMDAS. Each represents a sequence to follow when performing calculations to ensure consistency and precision.
This article breaks down what these acronyms stand for and how they are used in practice, making the world of math more manageable and less confusing.
What is BODMAS?
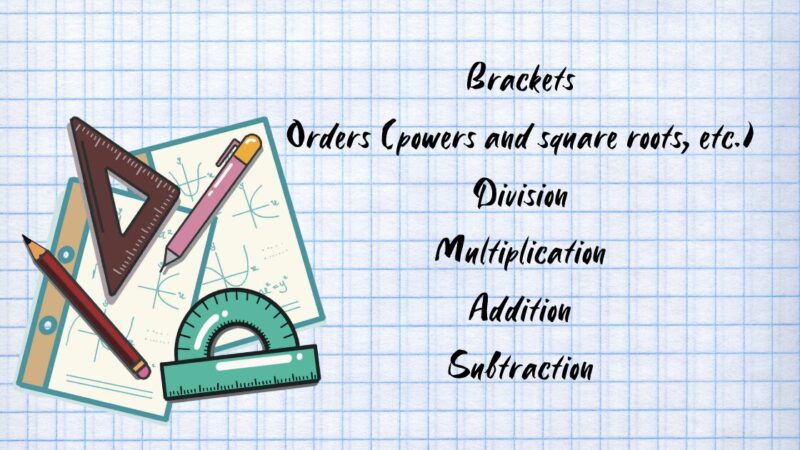
BODMAS serves as a guiding principle for solving mathematical expressions correctly.
- Brackets – Solve anything enclosed in parentheses, square brackets, or curly braces first.
- Orders – Address exponents, such as squares and square roots, before moving forward.
- Division and Multiplication – Process these operations next, moving left to right as they appear in the equation.
- Addition and Subtraction – Complete these steps last, again working from left to right.
Breaking Down BODMAS
Brackets (B)
Operations inside brackets should be handled first to simplify expressions before dealing with other calculations.
This applies to different types of brackets:
- ( ) – Parentheses
- [ ] – Square brackets
- { } – Curly braces
Example:
(5+3)×2
Solve the bracket first:
8×2=16
Orders (O)
Exponentiation (such as squaring numbers) or taking roots should be completed before moving to division and multiplication.
Example:
3(2)+4
Calculate the exponent first:
9+4=13
Division (D) and Multiplication (M)
Both operations should be performed as they appear in the equation, working left to right.
Example:
12÷4×3
Start with division:
3×3=9
Addition (A) and Subtraction (S)
Once multiplication and division are completed, addition and subtraction should be performed in the correct order.
Example:
10−2+4
Process left to right:
8+4=12
EXAMPLES
Example 1: Calculate 6+2×56 + 2 \times 56+2×5.
Following BODMAS:
- Multiplication first: 2×5=102 \times 5 = 102×5=10
- Then addition: 6+10=166 + 10 = 166+10=16
Example 2: Calculate 3×(2+4)23 \times (2 + 4)^23×(2+4)2.
Following BODMAS:
- Brackets first: 2+4=62 + 4 = 62+4=6
- Then Orders (exponent): 62=366^2 = 3662=36
- Finally, Multiplication: 3×36=1083 \times 36 = 1083×36=108
Example 3: Calculate (8−3)÷(2+1)(8 – 3) \div (2 + 1)(8−3)÷(2+1).
Following BODMAS:
- Brackets first: 8−3=58 – 3 = 58−3=5 and 2+1=32 + 1 = 32+1=3
- Then Division: 5÷3=1.675 \div 3 = 1.675÷3=1.67
What is BIDMAS?
BIDMAS is a mnemonic device that helps students and mathematicians remember the correct sequence for performing operations in mathematical expressions.
It serves the same function as BODMAS, with a slight variation in terminology.
- Brackets – Solve expressions inside parentheses first.
- Indices – Address exponents and roots next.
- Division and Multiplication – Process these operations in order, moving from left to right.
- Addition and Subtraction – Complete these last, also working from left to right.
Following BIDMAS ensures that calculations remain accurate and consistent, preventing misinterpretation of mathematical expressions.
By sticking to this sequence, mathematical problems are solved in a logical and structured manner.
Breaking Down BIDMAS
Brackets (B)
Solve expressions within brackets first, which can include parentheses ( ), square brackets [ ], and curly braces { }.
- Example: (4+2)×3=6×3=18(4 + 2) \times 3 = 6 \times 3 = 18(4+2)×3=6×3=18
Indices (I)
Next, calculate powers and roots.
- Example: 23+1=8+1=92^3 + 1 = 8 + 1 = 923+1=8+1=9
Division (D) and Multiplication (M)
These operations are performed from left to right, as they appear in the expression.
- Example: 16÷4×2=4×2=816 \div 4 \times 2 = 4 \times 2 = 816÷4×2=4×2=8
Addition (A) and Subtraction (S)
Finally, perform addition and subtraction from left to right.
- Example: 15−5+3=10+3=1315 – 5 + 3 = 10 + 3 = 1315−5+3=10+3=13
EXAMPLES
Example 1: Calculate 7+3×227 + 3 \times 2^27+3×22.
Following BIDMAS:
- Indices first: 22=42^2 = 422=4
- Then Multiplication: 3×4=123 \times 4 = 123×4=12
- Finally Addition: 7+12=197 + 12 = 197+12=19
Example 2: Calculate (5+3)÷4×2(5 + 3) \div 4 \times 2(5+3)÷4×2.
Following BIDMAS:
- Brackets first: 5+3=85 + 3 = 85+3=8
- Then Division: 8÷4=28 \div 4 = 28÷4=2
- Finally Multiplication: 2×2=42 \times 2 = 42×2=4
Example 3: Calculate 10−32+610 – 3^2 + 610−32+6.
Following BIDMAS:
- Indices first: 32=93^2 = 932=9
- Then Subtraction: 10−9=110 – 9 = 110−9=1
- Finally Addition: 1+6=71 + 6 = 71+6=7
What is PEMDAS?
PEMDAS is a well-known acronym in the United States, serving as a helpful way to recall the proper sequence for solving mathematical expressions.
- Parentheses – Perform calculations inside parentheses first.
- Exponents – Address any exponents or powers before moving on.
- Multiplication and Division – Solve these operations from left to right.
- Addition and Subtraction – Complete these last, also moving left to right.
By following this sequence, mathematicians, students, and professionals ensure that calculations are performed correctly and consistently.
Without a structured approach like PEMDAS, different methods of grouping numbers and operations could lead to varying results, creating confusion.
The system plays a crucial role in maintaining clarity across algebraic and arithmetic expressions, reinforcing precision in both basic and advanced mathematics.,
Breaking Down PEMDAS
Parentheses (P)
Solve any operations inside parentheses first. This can also include other types of brackets like square brackets [ ] and curly braces { }.
- Example: (3+5)×2=8×2=16(3 + 5) \times 2 = 8 \times 2 = 16(3+5)×2=8×2=16
Exponents (E)
Next, calculate powers and roots.
- Example: 42+1=16+1=174^2 + 1 = 16 + 1 = 1742+1=16+1=17
Multiplication (M) and Division (D)
These operations are performed from left to right, as they appear in the expression.
- Example: 20÷5×3=4×3=1220 \div 5 \times 3 = 4 \times 3 = 1220÷5×3=4×3=12
Addition (A) and Subtraction (S)
Finally, perform addition and subtraction from left to right.
- Example: 18−6+4=12+4=1618 – 6 + 4 = 12 + 4 = 1618−6+4=12+4=16
EXAMPLES
Example 1: Calculate 8+2×328 + 2 \times 3^28+2×32.
Following PEMDAS:
- Exponents first: 32=93^2 = 932=9
- Then Multiplication: 2×9=182 \times 9 = 182×9=18
- Finally Addition: 8+18=268 + 18 = 268+18=26
Example 2: Calculate (7−2)×4+6(7 – 2) \times 4 + 6(7−2)×4+6.
Following PEMDAS:
- Parentheses first: 7−2=57 – 2 = 57−2=5
- Then Multiplication: 5×4=205 \times 4 = 205×4=20
- Finally Addition: 20+6=2620 + 6 = 2620+6=26
Example 3: Calculate 12÷32−112 \div 3^2 – 112÷32−1.
Following PEMDAS:
- Exponents first: 32=93^2 = 932=9
- Then Division: 12÷9=1.3312 \div 9 = 1.3312÷9=1.33
- Finally Subtraction: 1.33−1=0.331.33 – 1 = 0.331.33−1=0.33
Key Differences
| Acronym | Region | Order | Example |
|---|---|---|---|
| BODMAS | UK, India, Commonwealth countries |
|
(2 + 3) × 4^2
= 5 × 16
= 80
|
| BIDMAS | UK, Australia, New Zealand |
|
(3 + 4) × 2^3
= 7 × 8
= 56
|
| PEMDAS | USA |
|
(1 + 2) × 3^2
= 3 × 9
= 27
|
Common Mistakes
When using BODMAS, BIDMAS, or PEMDAS, it’s easy to make mistakes that lead to incorrect results. Understanding these common pitfalls can help avoid errors and ensure accurate calculations.
Mastering BODMAS is essential for algebra students, as it helps simplify complex expressions correctly. For a structured approach to Algebra 1, check out this detailed introduction.
Misinterpreting the Order of Operations
A frequent mistake is misunderstanding the hierarchy of operations. This often happens when learners assume operations should be performed from left to right without following the specific order.
- Example: In the expression 6+2×36 + 2 \times 36+2×3, adding first (6 + 2 = 8) and then multiplying (8 × 3 = 24) is incorrect. The correct approach is to multiply first (2 × 3 = 6), then add (6 + 6 = 12).
Ignoring Parentheses
Another common error is ignoring or misplacing parentheses, which changes the intended order of operations.
- Example: For 8÷(4−2)×38 \div (4 – 2) \times 38÷(4−2)×3, if the parentheses are ignored, you might divide first (8 ÷ 4 = 2) and then subtract (2 – 2 = 0) and finally multiply (0 × 3 = 0). The correct way is to solve the parentheses first (4 – 2 = 2), then divide (8 ÷ 2 = 4), and finally multiply (4 × 3 = 12).
Mixing Up Division and Multiplication
Learners sometimes incorrectly believe that division should always come before multiplication because it appears first in the acronym.
- Example: In 12÷3×212 \div 3 \times 212÷3×2, performing the division first (12 ÷ 3 = 4) and then the multiplication (4 × 2 = 8) is correct. However, doing it the other way (3 × 2 = 6, then 12 ÷ 6 = 2) is incorrect.
Misplacing the Importance of Addition and Subtraction
Similar to division and multiplication, addition and subtraction must be performed from left to right, not based on the order in the acronym.
- Example: For 10−5+210 – 5 + 210−5+2, the correct method is to subtract first (10 – 5 = 5) and then add (5 + 2 = 7). Performing addition first (5 + 2 = 7, then 10 – 7 = 3) is incorrect.
Misunderstanding Exponents
Errors often occur when students misplace the position of exponents in the order of operations.
- Example: In 3×22+13 \times 2^2 + 13×22+1, calculating the exponent first (2^2 = 4), then multiplying (3 × 4 = 12), and finally adding (12 + 1 = 13) is correct. Multiplying first (3 × 2 = 6, then 6^2 = 36, and adding 1 to get 37) is incorrect.
Why the Order of Operations Matters
The order of operations is a fundamental principle in mathematics that ensures calculations are performed correctly and consistently. This principle is crucial for several reasons:
Ensures Consistency
The order of operations provides a standard procedure for solving mathematical expressions. Without it, different people might interpret and solve the same expression differently, leading to multiple answers for the same problem. This consistency is vital in fields that rely heavily on precise calculations, such as engineering, physics, and computer science.
- Example: In the expression 8+2×58 + 2 \times 58+2×5, without a standard order, one might add first (8 + 2 = 10, then 10 × 5 = 50) while another might multiply first (2 × 5 = 10, then 8 + 10 = 18). The correct order of operations ensures everyone calculates it as 8+10=188 + 10 = 188+10=18.
Avoids Ambiguity
Mathematical expressions often involve multiple operations. The order of operations removes ambiguity by specifying which operations to perform first. This clarity is essential for both simple arithmetic and complex algebraic expressions.
- Example: For the expression 3+6÷23 + 6 \div 23+6÷2, the correct interpretation is to divide first (6 ÷ 2 = 3), then add (3 + 3 = 6). Without the order of operations, one might add first (3 + 6 = 9) and then divide (9 ÷ 2 = 4.5), resulting in a different and incorrect answer.
Facilitates Complex Calculations
In advanced mathematics, calculations often involve nested operations and multiple levels of complexity. The order of operations allows mathematicians to break down complex problems into manageable steps, ensuring accuracy and coherence in their work.
- Example: In the expression (5+3)×22(5 + 3) \times 2^2(5+3)×22, following the order of operations, you first solve the parentheses (5 + 3 = 8), then the exponent (2^2 = 4), and finally the multiplication (8 × 4 = 32). This step-by-step approach simplifies solving complex expressions.
Essential for Technology and Programming
Computers and calculators use the order of operations to process mathematical instructions correctly. In programming, algorithms rely on these rules to execute commands in the proper sequence, ensuring that software functions as intended.
- Example: In programming, an expression like a+b×ca + b \times ca+b×c would be interpreted by the computer according to the order of operations, ensuring b×cb \times cb×c is calculated before adding aaa. Misinterpreting this order could lead to software bugs and incorrect outputs.
The Bottom Line
Understanding BODMAS, BIDMAS, and PEMDAS is essential for ensuring accurate and consistent mathematical calculations. These acronyms provide a clear framework for solving expressions by specifying the correct order of operations: Brackets/Parentheses first, followed by Orders/Exponents, then Division and Multiplication from left to right, and finally Addition and Subtraction from left to right.
By adhering to these rules, one can avoid common mistakes, reduce ambiguity, and achieve precise results in both simple and complex calculations.
