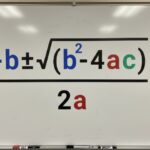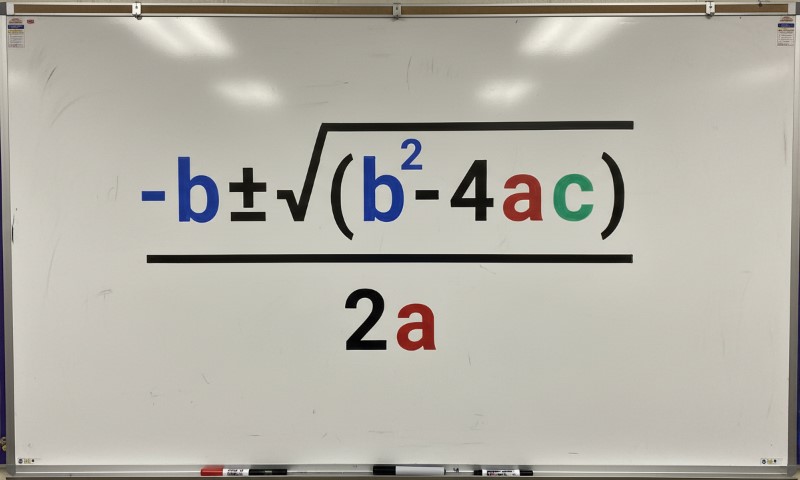Share Post:
Teaching math to kids can feel like walking a tightrope. You want them to stay curious, but you don’t want to pile on so much that they get lost or shut down. One thing that helps is introducing new ideas in small, bite-sized pieces they can actually chew on. Link what they’re learning to something they already get, let them practice right away, and give them room to move around and talk things out so they don’t zone out halfway through.
It also helps when kids understand why they’re learning something and how it fits into what they already know. If they’re in a space where making mistakes doesn’t feel like the end of the world, math becomes less intimidating—and sometimes, it even becomes something they look forward to.
Jo Boaler from Stanford and the NCTM have pointed out that a lot of math frustration happens because we rush, skip over the connections, or act like speed is the most important thing instead of real understanding. When you slow things down, build in scaffolding, and let students use both their hands and their minds, you can turn math time into a part of the day they actually enjoy, whether you’re at the front of a classroom or working through a problem together at the kitchen table.
Begin With What They Know
Why it helps: Students feel less stressed when they see how new concepts link to what they already understand.
How to do it:
- Pre-lesson warm-up: Spend 5–7 minutes revisiting a related skill. Before fractions, discuss everyday examples of sharing (pizza slices, dividing snacks).
- Visual links: Show how repeated addition connects to multiplication, like “3 + 3 + 3” is “3 x 3.”
- Prompt discussion:
- “Yesterday we regrouped in addition; today we’ll see regrouping in subtraction. Who remembers what regrouping means?”
- Before decimals, use dimes and pennies to relate to tenths and hundredths, letting students handle coins to bridge ideas.
Break Skills Into Micro-Steps
Why it helps: Prevents overwhelm, building mastery gradually.
In practice:
- Teaching long division:
- Review place value with base-ten blocks.
- Use repeated subtraction with small numbers.
- Move to partial quotients (e.g., 20 ÷ 4).
- Introduce the algorithm only after modeling repeatedly.
- Teaching fractions:
- Day 1: “What is a fraction?” with folding paper and sharing examples.
- Day 2: Identify fractions visually.
- Day 3: Place fractions on number lines.
- Day 4: Compare fractions with like denominators.
Use Visuals and Hands-On Tools
Why it helps: Many students need concrete visuals before they can handle abstract math confidently.
Practical tools:
- Fraction tiles for adding and comparing.
- Base-ten blocks for regrouping or decimals.
- Number lines for skip counting, fractions, or negatives.
Example activity: Before adding fractions, use fraction tiles so students can physically combine “1/4 + 1/4” instead of jumping to numeric calculation.
Visuals reduce fear of mistakes, encouraging experimentation.
Incorporate Movement and Discussion
Why it helps: Active learning keeps students engaged while reducing tension.
How to do it:
- Gallery walk: Post problems around the room for students to solve in pairs.
- Human number line: Have students stand in order while holding fraction cards.
- Math sorts: Give cards with examples and non-examples to sort and explain.
After movement, hold a 5-minute reflection for students to share how they solved problems, building reasoning and group learning.
Example: For even/odd numbers, let students sort number cards on the floor, then discuss why each belongs where it does.
Give Immediate, Encouraging Feedback
Why it helps: Stops misunderstandings from becoming habits while preserving confidence.
In practice:
- Use specific praise: “Great job lining up the decimals.”
- Gentle correction: “Good effort; let’s review the regrouping step together.”
- Guiding questions: “What does this digit represent in its place?”
During practice, circulate to note struggles and reteach as needed, providing guidance before mistakes stick.
Example: If a student adds “3.4 + 2.06” as “5.46,” review how to align decimals visually and let them retry immediately with support.
Provide Short, Focused Practice
Why it helps: Prevents overwhelm while reinforcing skills.
How to implement:
- Assign 5–7 targeted problems after modeling.
- Use exit tickets with one problem aligned with the skill.
- Allow practice on mini-whiteboards for easy correction without stress.
Example: After multiplying by 10, give students five numbers to multiply and share their answers aloud, reinforcing place value shifts.
Small, repeated practice builds automaticity without anxiety.
Use Technology for Reinforcement
Technology can enhance practice in a low-pressure, engaging way. This includes:
- Interactive math games to reinforce skills.
- Video explanations for additional perspectives.
- A math equation generator to create customized practice problems at appropriate difficulty, allowing immediate, adaptive practice while you monitor progress.
Using a math equation generator allows you to generate tailored, scaffolded problems live during teaching or homework, matching student readiness and helping them move forward without being overwhelmed.
Celebrate Effort and Growth
Why it helps: Focusing on progress reduces fear of mistakes.
Practical ways:
- Use growth charts to track skills.
- Offer verbal praise like, “You stuck with that tough problem.”
- Let students showcase strategies on the board.
- Send home quick notes celebrating specific wins.
Pause and Reteach as Needed
View this post on Instagram
Why it helps: Pushing ahead too quickly creates confusion and math anxiety.
When to pause:
- Multiple students making the same error.
- Confidence drops or mistakes increase.
- Exit tickets show gaps in understanding.
What to do:
- Revisit the concept with visuals or manipulatives.
- Let students share what’s confusing.
- Review prerequisites before reintroducing the new skill.
Example: If regrouping in subtraction causes issues, go back to using base-ten blocks before returning to abstract problems.
Final Thoughts
Teaching new math skills does not have to cause stress for you or your students. By connecting new concepts to prior knowledge, breaking them into manageable parts, using visuals and discussion, and providing immediate feedback, you create an environment where mistakes are part of growth, not something to fear.
Short, focused practice and tailored problems using tools like a math equation generator will help you meet
