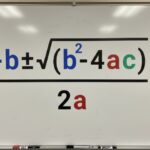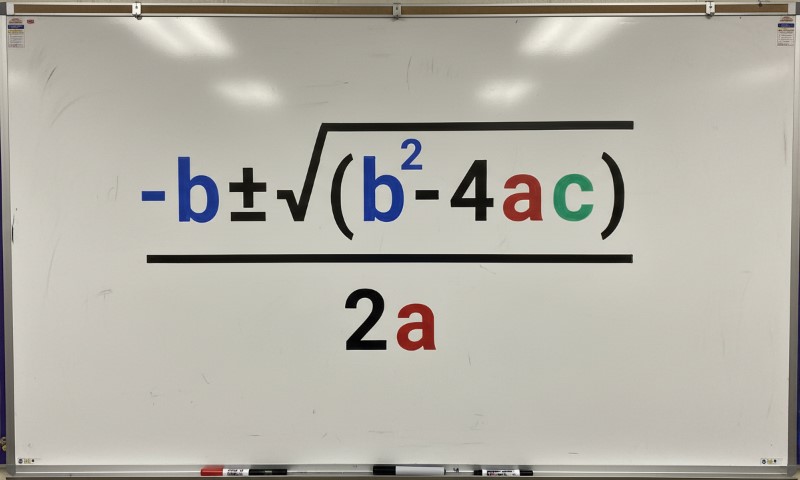Share Post:
Supporting children as they shift from arithmetic to algebra sets the tone for future success in mathematics.
Early mastery builds confidence, while poor transitions can lead to long-term struggles.
Addressing math-related anxiety early and fostering curiosity can ease the shift and make learning algebra a more natural progression.
Building a Strong Arithmetic Foundation
Before algebraic thinking can take root, children need a firm grasp of essential arithmetic skills. Rapid number recognition, often referred to as subitising, builds mental agility.
Number bonds to 10 reinforce how numbers relate to each other, setting a base for future equations.
Automaticity in basic operations frees cognitive space. When addition, subtraction, multiplication, and division become second nature, attention can shift to new ideas instead of mechanics.
Place value, often described as the “10-ness of 10,” reveals number structure and prepares students for abstract reasoning.
Re-teaching the meaning helps establish essential mental models for algebra.
Several early learning concepts directly influence algebra readiness. Introduce the following to build logical thinking:
- Pattern recognition: spotting sequences, changes, and repetitions
- Spatial reasoning: visualizing how parts relate and transform
- Composition and comparison: combining elements and assessing relationships
To guide children through stages of understanding, use the CPA (Concrete–Pictorial–Abstract) method. Encourage progression with:
- Concrete materials: cubes, counters, and other manipulatives
- Pictorial models: bar diagrams, drawn representations
- Abstract symbols: equations and variables
Confidence grows when children move through these stages with clarity and support, which can be reinforced through sessions with a maths tutor who understands early arithmetic needs.
Introducing the Language of Algebra
Algebra often carries an aura of confusion, but it simply expresses unknowns and relationships in a structured form.
Introducing children to algebra as a way to solve puzzles shifts focus away from memorized steps toward curiosity and reasoning.
Letters such as x or y act as placeholders, not mysterious symbols.
Framing them within problems children already know, like turning “2 + ? = 5” into “2 + x = 5,” makes the new language feel familiar.
Key points to highlight include:
- Variables as placeholders: letters that represent numbers yet to be found
- Equations as puzzles: algebra helps discover what value makes an equation true
- Contextual continuity: arithmetic skills flow into algebra naturally with a shift in notation
Children who solve missing number problems are already engaged in algebraic reasoning.
Making that connection explicit helps remove anxiety and builds excitement.
Familiarity leads to confidence, and confidence leads to more willing learners.
Step-by-Step Instructional Strategy
Introducing algebra to children works best through deliberate, scaffolded teaching.
A smooth transition requires thoughtful progression. Strategies must engage curiosity, promote logical reasoning, and connect new learning to what students already know.
Several key methods outlined below support this shift.
1. Use Visual and Concrete Representations (CPA Method)
Physical tools anchor abstract thinking in real-world experience. Children benefit from using tangible items before advancing to symbols.
- Begin with manipulatives: counters, cubes, base-ten blocks, or ten frames.
- Move to visual models: bar diagrams, number lines, or part-whole representations.
- Introduce abstract forms: letters, symbols, and algebraic expressions.
2. Introduce Patterns and Relationships
Patterns help children make sense of structure. Repeated sequences form the basis for algebraic thinking.
- Use color or shape patterns to build visual intuition.
- Introduce growing number patterns, like 2, 4, 6 or 5, 10, 15.
- Ask guiding questions: “What comes next?” or “How does this grow?”
These activities teach children to identify change and apply reasoning.
Recognizing consistent rules in patterns prepares students for functions and expressions later on.
3. Teach the Concept of Unknowns
Algebra often involves solving for a missing value. Presenting problems as puzzles keeps students engaged.
- Use simple expressions: x + 5 = 10, 12 – x = 7.
- Reinforce the balance concept: equal signs represent both sides having the same value.
- Emphasize logical thinking over guessing.
Unknowns become less intimidating when introduced gradually.
Allowing students to discover solutions through guided questions builds confidence.
4. Encourage Verbal Reasoning and Math Talk
Thinking becomes clearer through conversation.
Verbalizing strategies deepens comprehension and promotes reflection.
- Ask students: “What did you do?” or “Why did you do that?”
- Encourage multiple approaches: “Can you think of another way?”
- Create a safe space for errors and revisions.
Expressing thought processes aloud helps students internalize problem-solving strategies.
Hearing others’ methods also introduces new ways of thinking.
5. Gradual Complexity
Success starts with accessible problems. Starting simple allows students to build confidence before moving into more complex equations.
- Start with one-step problems: x + 3 = 6, 8 – x = 2.
- Move to two-step problems: 2x + 3 = 7, 3x – 4 = 5.
- Introduce relatable scenarios: sharing cookies equally, measuring ingredients, or adjusting recipes.
Using everyday examples makes math meaningful. Students learn that algebra isn’t separate from real life but a tool to describe it.
Overcoming Cognitive Load Challenges
Helping children transition into algebraic thinking requires more than solid instruction and engaging activities. It demands attention to how much their minds can process at once.
Young learners have limited working memory, and too many ideas presented too quickly can create cognitive overload.
To support successful learning, educators and parents need to be strategic in how information is delivered.
Several practical approaches grounded in Cognitive Load Theory can reduce strain and improve retention.
Break Problems into Manageable Parts
Small chunks of information are easier to digest. Instead of presenting an entire equation-solving process in one go, introduce one step at a time.
Allow time for children to process, practice, and master before moving forward.
- Use color-coding to highlight parts of an equation
- Break down problems verbally and visually
- Ask guiding questions like “What should we do first?”
Focus Only on Essential Information
Too much detail or extra content can create confusion. Narrowing focus to what matters most helps children form clear mental structures.
- Remove unnecessary decorations or unrelated images from worksheets
- Use consistent and simple language when giving instructions
- Highlight key words or symbols to reduce distraction
Minimize Distractions
Environmental noise, visual clutter, or poorly organized materials can interfere with focus.
A calm, structured learning environment supports mental clarity.
- Organize desks and materials neatly before starting an activity
- Use plain backgrounds on slides or whiteboards
- Establish quiet routines before instruction begins
Activities to Reinforce Algebraic Thinking
View this post on Instagram
Engaging activities help solidify skills. Matching games pair equations with answers, encouraging pattern recognition and logic. “Guess the number” riddles with equations spark interest and challenge children to think flexibly.
Building patterns with blocks or colored paper can reinforce structure. Using digital apps that break down algebra into interactive steps keeps learners engaged and allows self-paced exploration.
Varied activities appeal to different learning styles. Some students need to move and build, others benefit from visuals or games.
The Bottom Line
Progression to algebra doesn’t happen in a single step. Children move gradually through experiences that connect arithmetic to more abstract reasoning.
Strong arithmetic skills, thoughtful instruction, and fun activities help students grow into confident algebra thinkers.
Support and encouragement from both teachers and families ensure no child feels left behind in math.
