Share Post:
The Fibonacci sequence is a simple pattern of numbers where each number is the sum of the two numbers before it. It starts like this:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34 … and it continues forever.
So if you add 2 and 3, you get 5. If you add 5 and 8, you get 13. That’s all there is to the rule.
This sequence was made famous over 800 years ago by Leonardo of Pisa, also called Fibonacci, who used it to solve a problem about rabbits having babies. What makes it special is that this number pattern doesn’t just live in math books; it shows up in the petals of flowers, the spiral of seashells, the way pinecones grow, the shapes of galaxies, the design of famous buildings, and even music and art.
For kids, the Fibonacci sequence is one of the best examples of how math is not just about worksheets; it is a language of patterns that explains how the world grows and organizes itself.
Table of Contents
ToggleWho Was Fibonacci?
Leonardo of Pisa, better known as Fibonacci, lived in Italy in the late 1100s and early 1200s. At that time, most of Europe still used Roman numerals, which made math difficult. Fibonacci traveled to North Africa with his merchant father and learned the Hindu-Arabic numeral system, the one we use today with 0–9.
In 1202, he wrote a book called Liber Abaci (Book of Calculation), which introduced this new system to Europe. Inside that book was a famous puzzle about rabbits. He asked:
- If you start with one pair of rabbits, and each pair produces a new pair every month, how many pairs will there be after a year?
When he solved it, the numbers followed a pattern we now call the Fibonacci sequence.
The Rule of the Fibonacci Sequence
The Fibonacci sequence has only one rule:
Add the two previous numbers to get the next number.
Step by step:
- Start with 0 and 1.
- 0 + 1 = 1
- 1 + 1 = 2
- 1 + 2 = 3
- 2 + 3 = 5
- 3 + 5 = 8
- 5 + 8 = 13
- … and it goes on forever.
First Fibonacci Numbers

Here’s a table showing the first 15 numbers:
| Position (n) | Fibonacci Number |
| 0 | 0 |
| 1 | 1 |
| 2 | 1 |
| 3 | 2 |
| 4 | 3 |
| 5 | 5 |
| 6 | 8 |
| 7 | 13 |
| 8 | 21 |
| 9 | 34 |
| 10 | 55 |
| 11 | 89 |
| 12 | 144 |
| 13 | 233 |
| 14 | 377 |
Notice how quickly the numbers get large. That’s because each number builds on the last two.
Fibonacci in Nature: Fun, Concrete Examples

The Fibonacci sequence is more than numbers. It describes how things grow. Kids can spot it outside, in food, and even in the mirror.
1. Flowers and Petals
Many flowers have Fibonacci numbers of petals:
- Lilies → 3 petals
- Buttercups → 5 petals
- Daisies → 34 or 55 petals
- Sunflowers → hundreds of petals, often in Fibonacci spirals
This happens because Fibonacci growth helps plants spread petals evenly, so each petal gets sunlight.
2. Pinecones, Pineapples, and Sunflowers
If you look at the bottom of a pinecone or a pineapple, you’ll see scales arranged in spirals. Count them: one spiral goes one way, another goes the opposite way. Often, the numbers are 8 and 13, or 21 and 34, or 34 and 55, all Fibonacci numbers.
Sunflowers show this even more clearly. The seeds in the middle grow in crisscross spirals, and when you count them, the numbers almost always come from the sequence. This helps seeds pack tightly without wasting space.
3. Seashells and Spirals
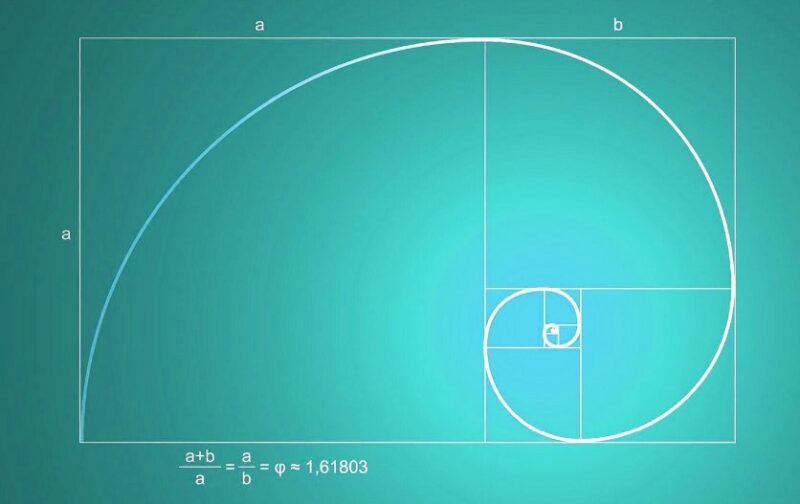
The nautilus shell is a perfect example. Each new section grows wider, but in exact proportion to the Fibonacci sequence. When you draw squares with side lengths from Fibonacci numbers and connect curves through them, you get the same spiral.
Even hurricanes and galaxies form spiral arms close to Fibonacci proportions.
4. Animal Features
@piomath0 Mathematics and History: Fibonacci’s Rabbits. In Liber Abaci, published in 1202, Leonardo Fibonacci reports this problem. “A man placed a pair of rabbits in a place completely surrounded by walls, to discover how many pairs of rabbits would descend from them in a year. By nature, every month the pairs of rabbits generate another pair and begin to procreate in the second month after birth.” In the video, you can see that the sequence obtained, if you consider the number of rabbits pairs month after month, is precisely the Fibonacci Sequence! #math #maths #for #foruyou #edit #fyp #phonk #perte #perteeee
- Rabbits in Fibonacci’s puzzle grow in Fibonacci numbers.
- The branching of deer antlers often follows Fibonacci growth.
- The horns of rams curve in spirals that match Fibonacci patterns.
- Even the way DNA twists (a double helix) relates to Fibonacci proportions.
5. The Human Body
The Fibonacci sequence also shows up in us:
- We have 1 nose, 2 eyes, and 5 fingers on each hand.
- Our hands show Fibonacci in bone lengths: each bone is roughly 1.6 times the length of the one before (the Golden Ratio, which comes from Fibonacci).
- The spiral of the ear and hair whorls also match Fibonacci spirals.
6. Art and Architecture
Artists and builders use Fibonacci to make designs that look pleasing to the eye. The Golden Rectangle, made from Fibonacci numbers, is used in paintings, buildings, and logos.
Examples:
- The Parthenon in Athens
- The pyramids in Egypt
- The Mona Lisa by Leonardo da Vinci
- Apple’s old logo design proportions
7. Music and Rhythm
Composers sometimes use Fibonacci numbers in rhythm, melody, and harmony. A song may have phrases of 8 or 13 beats. The way a piece builds and then changes can follow Fibonacci timing. Kids can try clapping rhythms of 1, 2, 3, 5, and 8 beats to feel the sequence in music.
Drawing Fibonacci: Step by Step
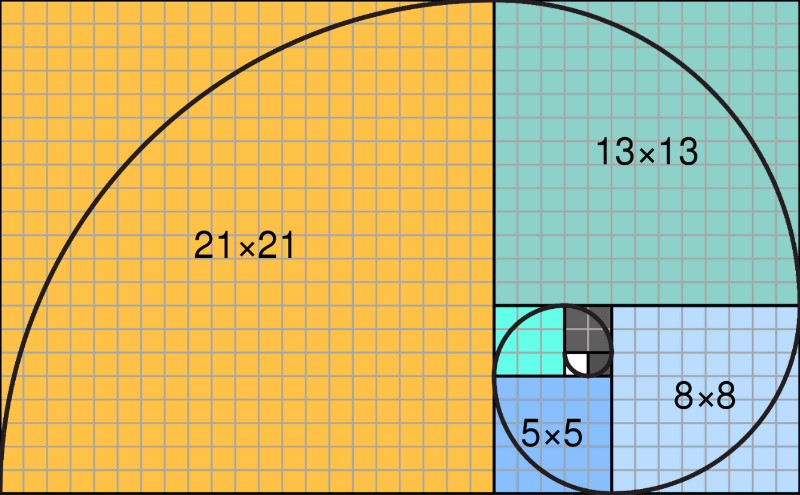
One of the best activities for kids is drawing a Fibonacci spiral.
- Draw a 1×1 square.
- Draw another 1×1 square next to it.
- Draw a 2×2 square on top.
- Draw a 3×3 square next to those.
- Draw a 5×5 square underneath.
- Keep going with 8×8, 13×13, etc.
- Now, draw a quarter-circle arc in each square.
When you connect them, you’ll see a spiral that looks just like shells and flowers.
Fibonacci and the Golden Ratio
The Fibonacci sequence leads to the Golden Ratio. This is a special number: 1.618… (goes on forever).
If you divide one Fibonacci number by the one before it, the answer gets closer and closer to 1.618.
Examples:
- 8 ÷ 5 = 1.6
- 13 ÷ 8 = 1.625
- 21 ÷ 13 = 1.615
The Golden Ratio is found in nature and design because it balances growth and beauty.
Why the Fibonacci Sequence Matters for Kids

- It makes math real. Instead of being just numbers, kids can see Fibonacci in flowers, shells, and animals.
- It shows patterns. Math is about finding patterns, and Fibonacci is one of the easiest to see.
- It builds curiosity. Kids start asking, “Where else can I see this?” and notice more about the world.
- It links subjects. Fibonacci connects math, science, art, music, and even history.
- It’s fun. Drawing spirals, counting petals, and spotting Fibonacci make learning playful.
Real-Life Examples Table
| Everyday Object | Fibonacci Connection |
| Sunflower | Seeds form spirals of 34 and 55 (both Fibonacci). |
| Pineapple | Diamond shapes in spirals match Fibonacci numbers. |
| Pinecone | Spiral rows of scales follow Fibonacci numbers. |
| Nautilus shell | Grows outward in Fibonacci spirals. |
| Flowers | 3, 5, 8, 13 petals, Fibonacci numbers. |
| Human hand | 5 fingers, each with 3 parts, proportions near Fibonacci. |
| Galaxies | Spiral arms grow in Fibonacci-like curves. |
| DNA | Helix turns are related to Fibonacci ratios. |
Activities for Kids

- Petal hunt: Go outside, pick flowers, and count the petals. Do they match Fibonacci numbers?
- Pinecone puzzle: Look at a pinecone and count the spirals. Try to find Fibonacci numbers.
- Spiral art: Use graph paper and crayons to draw Fibonacci squares and spirals.
- Rabbit game: Pretend you have pairs of rabbits multiplying like Fibonacci’s puzzle. Keep track of the numbers.
- Music beats: Clap 1, 2, 3, 5, and 8 beats in a row to feel the sequence.
Conclusion
The Fibonacci sequence starts simply: each number is the sum of the two before it. But this small rule leads to amazing patterns all around us. Kids can see it in flowers, pinecones, seashells, animals, art, music, and even in their own bodies.
Learning Fibonacci shows that math is not just about calculation, it’s about recognizing the hidden order of nature and design. Every time you spot a spiral in a shell, or count the petals of a flower, you can remember that math is alive in the world.
Related Posts:
- Prime Numbers Explained For Kids With Easy Examples…
- What is a Point in Geometry? Definition and Examples
- What Are the Types of Polynomials? Definitions and Examples
- Complete Guide to Teaching Math with Base 10 Blocks…
- Natural Numbers - Definition, Properties, and Examples
- What Are Irrational Numbers - Definition, Examples &…