Share Post:
In mathematics, numbers are often grouped based on how they behave when divided by other numbers. Composite numbers belong to a fundamental yet important group. A composite number must meet two conditions at the same time.
First, it must be greater than 1. Second, it must have more than two positive factors. Factors are whole numbers that divide into another number with no remainder. Because of this rule, numbers like 4, 6, 8, 9, 10, and 12 are all composite.
This idea is taught early in school because it connects directly to multiplication, division, fractions, and later algebra.
According to standard elementary math curricula used in the United States, the United Kingdom, and many EU countries, students are expected to identify composite numbers reliably by grades 3 or 4, usually between ages 8 and 10.
Understanding composite numbers helps students break numbers apart, understand equal groups, and recognize patterns in multiplication tables.
Factors Explained in a Clear Way
To understand composite numbers, factors must be understood first. A factor is any whole number that divides another whole number evenly.
For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. Because 12 has more than two factors, it is composite.
This table shows how factors determine whether a number is composite.
Factors and Number Type
Number
Factors
Total Factors
Number Type
2
1, 2
2
Prime
3
1, 3
2
Prime
4
1, 2, 4
3
Composite
5
1, 5
2
Prime
6
1, 2, 3, 6
4
Composite
8
1, 2, 4, 8
4
Composite
9
1, 3, 9
3
Composite
This structure shows a clear rule. If a number has only two factors, it is prime. If it has more than two, it is composite.
Composite Numbers Versus Prime Numbers
Composite numbers are often explained together with prime numbers because they are opposites in one important way. A prime number has exactly two factors.
A composite number has more than two factors. This contrast helps students remember the difference.
Prime numbers act like building blocks in math. Composite numbers are built from those blocks. For example, 10 is composite because it equals 2 ร 5. Both 2 and 5 are prime numbers.
This relationship becomes essential later when students learn prime factorization.
Prime and Composite Comparison
Feature
Prime Numbers
Composite Numbers
Smallest example
2
4
Number of factors
Exactly 2
More than 2
Can be multiplied by
Only 1 ร itself
Two or more numbers
Used as building blocks
Yes
No
Examples under 20
2, 3, 5, 7, 11, 13, 17, 19
4, 6, 8, 9, 10, 12, 14, 15
Understanding this difference early prevents confusion later when topics like fractions, greatest common factor, and least common multiple are introduced.
Why the Number 1 Is Not Composite
A common question from kids is whether the number 1 is composite. It is not. The reason is very specific. The number 1 has only one factor, which is itself.
Composite numbers must have more than two factors, and prime numbers must have exactly two. Because 1 does not fit either rule, it is placed in its own category.
This rule is not arbitrary. It has been part of formal mathematics since the 19th century, when mathematicians agreed on definitions that would make number theory consistent.
Without this rule, many theorems involving prime and composite numbers would not work correctly.
How to Identify Composite Numbers Step by Step
View this post on Instagram
To identify a composite number, students are usually taught a simple method. First, check whether the number is greater than 1. Second, test whether it can be divided evenly by any number other than 1 and itself. If it can, the number is composite.
For example, take the number 15. It is greater than 1. It can be divided evenly by 3 and 5. That means it has four factors: 1, 3, 5, and 15. Because of this, 15 is composite.
This process strengthens division skills and prepares students for factor trees and multiplication strategies used later in school.
Composite Numbers and Multiplication Tables
Composite numbers appear constantly in multiplication tables. Any number that can be made by multiplying two smaller whole numbers greater than 1 will be composite.
For example, every result in the 4, 6, 8, 9, and 10 times tables is composite except when multiplied by 1.
Multiplication
Result
Composite
2 ร 3
6
Yes
3 ร 4
12
Yes
4 ร 5
20
Yes
5 ร 6
30
Yes
3 ร 7
21
Yes
This connection explains why composite numbers are so common in everyday math problems involving equal groups or repeated addition.
Composite Numbers in Real School Math
Composite numbers are not taught just as definitions. They appear in real classroom tasks. When students simplify fractions, they use composite numbers to find common factors.
When they calculate area, composite side lengths allow multiple rectangle shapes. When they work with arrays, composite numbers allow more than one arrangement.
Educational research from national math standards bodies shows that students who understand factor-based number types earlier perform better in later arithmetic and algebra tasks. Composite numbers are part of that foundation.
Common Mistakes Kids Make
One frequent mistake is thinking that all even numbers are composite. This is almost true, but not completely. The number 2 is even, but it is prime.
Another common error is assuming that large numbers are always composite. In reality, numbers like 101 or 103 are prime even though they are large.
These mistakes happen because students rely on patterns without checking factors. That is why practicing factor checking is important.
Practice Questions With Structured Tables
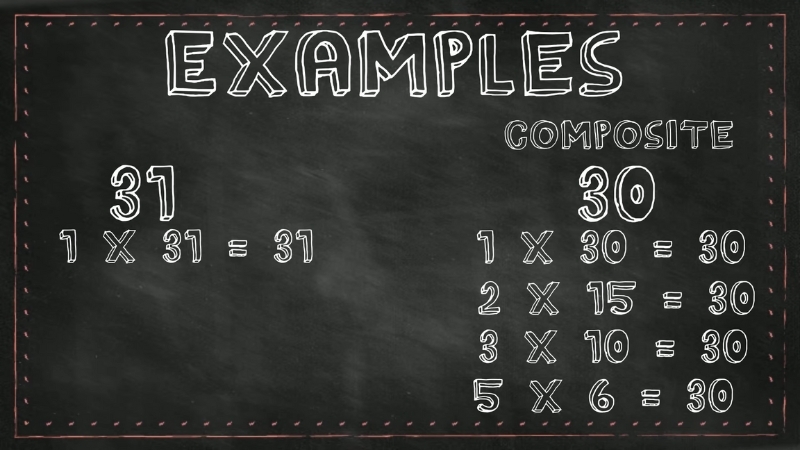
Identify Composite Numbers
Number
Composite or Not
Reason
7
9
11
14
16
Students should fill in whether each number is composite and list at least one factor besides 1 and itself if it is composite.
Practice: Counting Factors
Number
List All Factors
Total Factors
Composite
8
10
13
18
This exercise builds accuracy and helps students connect the idea of factors directly to classification.
Mixed Practice With Explanation
Number
Prime
Composite
Neither
1
2
4
17
21
This format reinforces that not all numbers fit into only two categories and helps students understand why 1 is special.
Final Clarification
@dylanlimfj Sec 1 Numbers – Composite Numbers #mathtok #secondary #singapore #secondary1 #math โฌ Background Music – chill supply
Composite numbers are whole numbers greater than 1 that have more than two factors. They can be divided evenly in more than one way and are built from smaller numbers through multiplication.
Learning to identify them strengthens number sense, improves division and multiplication skills, and prepares students for more advanced math topics that rely on factor relationships.
