Share Post:
The Box Method for factoring is a visual and organized approach to factoring trinomials, particularly quadratics.
It involves breaking down a polynomial into smaller parts using a 2×2 grid, or “box,” to organize terms for easy manipulation.
We are talking about a method that is especially helpful when the leading coefficient (the coefficient in front of the squared term) is not 1, making the factoring process clearer.
It serves as a reliable tool to minimize errors and ensures that all factor pairs are considered, making it a favorite among students learning how to factor quadratics efficiently.
Let us talk about it.
Basic Steps in the Box Method
The Box Method begins by organizing the quadratic equation into the form ax2+bx+cax^2 + bx + cax2+bx+c, where aaa, bbb, and ccc are the coefficients of the equation.
Here are the steps to follow:
- Check for a GCF (Greatest Common Factor):
Before proceeding, examine the terms of the quadratic equation to see if a GCF exists. If there is one, factor it out to simplify the expression. - Draw the 2×2 Grid (Box):
Once the equation is simplified (or if no GCF exists), draw a 2×2 grid.- The top-left box will contain the first term ax2ax^2ax2.
- The bottom-right box will hold the constant ccc.
- Multiply the Leading Coefficient and the Constant:
Multiply aaa (the coefficient of x2x^2×2) by ccc (the constant). This product is critical for the next step. - Identify Two Numbers:
Find two numbers that multiply to the product of a×ca \times ca×c but also add up to bbb, the coefficient of the middle term.- These numbers will be placed in the remaining two boxes of the grid.
- Factor Rows and Columns:
Once all boxes are filled, determine the GCF for each row and column.- The GCF of each row and column is written outside the corresponding side of the grid.
- Write the Final Factors:
The result from factoring rows and columns will reveal the factored version of the original quadratic expression.
A structured approach simplifies factoring and minimizes mistakes, making the process more intuitive.
Worked Examples
Now let us address the worked examples:
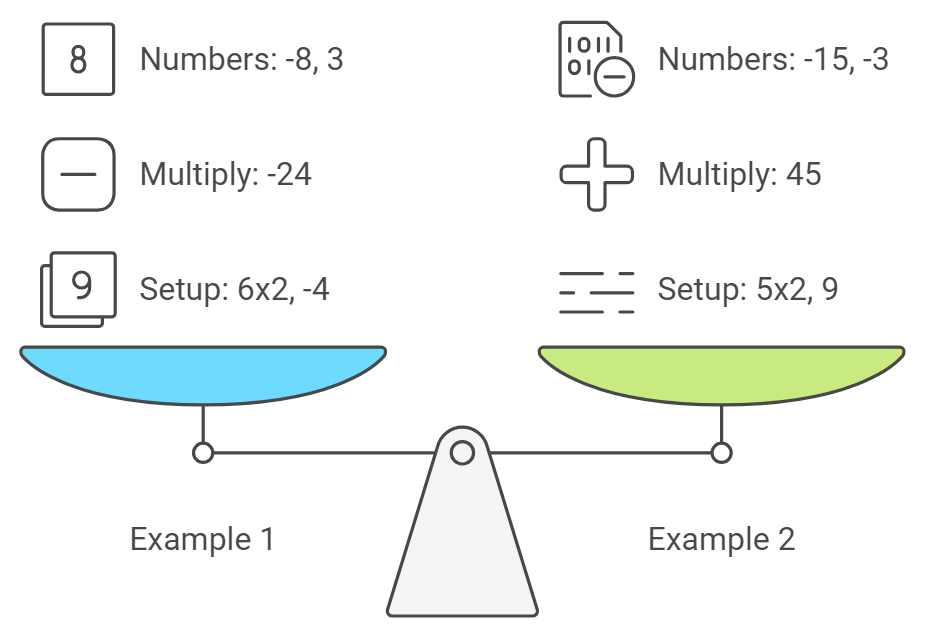
Example 1: Factoring 6×2−5x−46x^2 – 5x – 46×2−5x−4
Start by setting up the quadratic equation 6×2−5x−46x^2 – 5x – 46×2−5x−4. The first term, 6x26x^26×2, goes in the top-left box, and the constant, −4-4−4, goes in the bottom-right box. Multiply 6×−4=−246 \times -4 = -246×−4=−24.
Now, find two numbers that multiply to -24 and add up to -5 (the middle term). These numbers are -8 and 3. Place them in the remaining two boxes.
Once the grid is filled, find the GCF for each row and column. The GCFs for the rows are 2x2x2x and -2, and for the columns, the GCFs are 3x3x3x and -1. Therefore, the factored form of 6×2−5x−46x^2 – 5x – 46×2−5x−4 is (3x+2)(2x−2)(3x + 2)(2x – 2)(3x+2)(2x−2).
Example 2: Factoring 5×2−18x+95x^2 – 18x + 95×2−18x+9
With this example, 5x25x^25×2 goes in the top-left box and 9 in the bottom-right box. Multiply 5×9=455 \times 9 = 455×9=45. Now, find two numbers that multiply to 45 and add up to -18. These numbers are -15 and -3.
Fill the remaining boxes with these numbers, then find the GCF for each row and column. The result will be (5x−3)(x−3)(5x – 3)(x – 3)(5x−3)(x−3).
Example 3: Factoring with Common Factors
Consider a quadratic like 8×2+12x+48x^2 + 12x + 48×2+12x+4. Here, the first step is factoring out the GCF of 4, resulting in 4(2×2+3x+1)4(2x^2 + 3x + 1)4(2×2+3x+1).
Then, use the Box Method to factor 2×2+3x+12x^2 + 3x + 12×2+3x+1. The box will reveal the factors (2x+1)(x+1)(2x + 1)(x + 1)(2x+1)(x+1), making the final factored form 4(2x+1)(x+1)4(2x + 1)(x + 1)4(2x+1)(x+1).
Common Pitfalls to Avoid
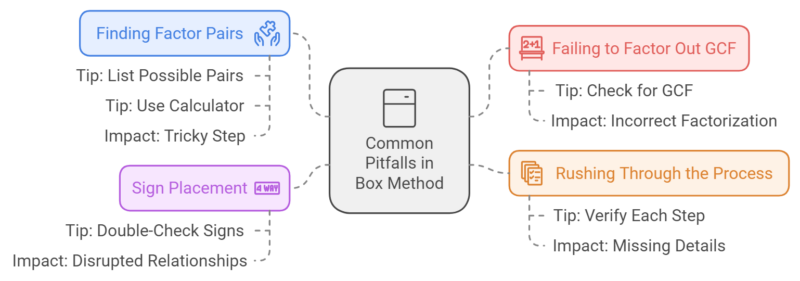
When using the Box Method for factoring, there are several common pitfalls that can hinder the correct solution if not addressed properly. Awareness of these issues can save time and prevent frustration, ensuring a smooth factoring process.
One of the most frequent mistakes is failing to factor out the greatest common factor (GCF) before setting up the grid. Factoring out the GCF simplifies the polynomial and reduces the complexity of the terms involved.
If the GCF is not considered at the beginning, the entire factorization can be incorrect because the terms in the grid will not reflect the simplest form of the polynomial.
- Tip: Always start by checking for a GCF. If all terms share a common factor, factor it out before proceeding with the Box Method.
Another common error occurs when finding the factor pairs after multiplying the leading coefficient aaa and the constant ccc. Students often struggle to identify two numbers that not only multiply to this product but also add up to the middle-term bbb. This step can be tricky, especially when the product is large or involves negative values.
- Tip: If you cannot immediately identify the correct factor pair, try listing out all the possible pairs for the product of a×ca \times ca×c and test which one adds to bbb.
- Tip: If necessary, use a calculator or multiplication chart to verify factor pairs. This can prevent errors caused by incorrect mental calculations.
Finally, a subtle yet significant pitfall is rushing through the process without rechecking each step. Many students feel confident once they have filled in the grid but neglect to confirm their results. This oversight can lead to missing small but crucial details like incorrectly factoring out rows or columns.
- Tip: After filling in the grid, go over your factorization process by verifying the terms in each row and column to ensure accuracy. Double-check the GCF for both rows and columns before writing out the final factors.
Sign Placement
Sign placement is another key area where mistakes frequently occur. When filling in the boxes of the grid, it’s essential to pay close attention to positive and negative signs. Misplacing a negative sign can lead to incorrect factorization because the relationships between the terms will be disrupted.
-
- Tip: Double-check the signs when placing each term in the grid. If the equation includes negative coefficients, ensure they are correctly reflected in the grid setup.
Benefits of the Box Method
The Box Method for factoring offers a range of advantages over traditional factoring techniques. Its systematic approach provides clarity and accuracy, making it a preferred method for both beginners and experienced mathematicians alike. Here are some key benefits that make the Box Method stand out:
| Benefit | Description |
|---|---|
| Visual and Organized Structure | Organizes terms in a grid to highlight interactions and common factors. |
| Reduces Errors | Reduces errors by following a clear step-by-step process. |
| Works for Quadratics with a Leading Coefficient Greater Than 1 | Simplifies complex quadratics with leading coefficients greater than 1. |
| Systematic Approach for Both Simple and Complex Problems | Works for both simple and complex quadratics systematically. |
| Adaptable to Higher-Degree Polynomials | Can be adapted for higher-degree polynomials. |
Applications of the Box Method
The Box Method can be extended beyond quadratic equations to handle higher-degree polynomials, such as cubic equations.
The concept remains the same, breaking down the polynomial into smaller, manageable terms and organizing them into a grid.
For example, when factoring a cubic polynomial, a 3×3 grid might be used instead of a 2×2 grid. The same principles apply, with each box in the grid holding a term from the polynomial and the GCFs of the rows and columns revealing the factors.
The Box Method’s flexibility makes it useful for a wide range of factoring problems, providing students with a consistent, reliable tool for algebraic manipulations.
The box method breaks down complex quadratics into simpler parts, making them easier to solve. Laying the terms in a grid helps you see how they interact. Understanding how elements relate can also help with properties like equivalence relations, where spotting patterns makes problem-solving easier.
Summary
The Box Method simplifies the process of factoring by offering a structured and visual approach. It reduces the likelihood of errors and works well for factoring a wide variety of quadratic and higher-degree polynomials.
With practice, students can become proficient in using this method, improving their ability to solve polynomial equations efficiently and accurately.
The more you know: The number 1 is not a prime number. Why or how you ask? Find out more!
