Share Post:
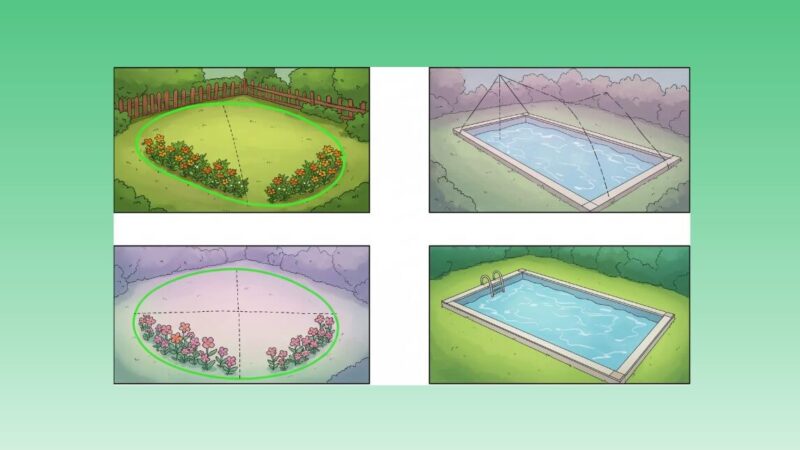
The clear answer is this: Perimeter tells us how far it is all the way around a shape. Area tells us how much space is inside the shape.
Think about a school playground. If you walk along the fence that goes all the way around the playground, you are measuring the perimeter. But if you look at how much ground is inside the fence where kids can run, play soccer, or draw with chalk, you are talking about the area. Both use numbers to describe a shape, but they measure very different things.
Table of Contents
ToggleWhat Is Perimeter?
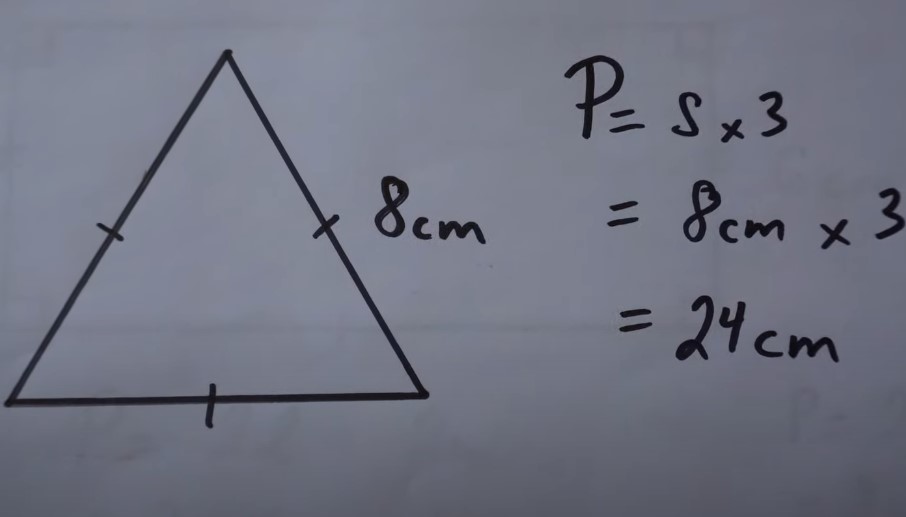
The perimeter is like the outline of a shape. To find it, you add up the lengths of all the sides.
- For a square, it is easy: just one side length × 4.
- For a rectangle, you add the two lengths and two widths together.
- For a circle, the perimeter is called the circumference, and you find it using a special number called pi (π).
Example 1: Rectangle
A rectangle that is 10 meters long and 5 meters wide has a perimeter of:
10 + 5 + 10 + 5 = 30 meters.
That means if you wanted to put a fence around the rectangle, you would need 30 meters of fencing.
Example 2: Triangle
If a triangle has sides of 4 cm, 5 cm, and 6 cm, then the perimeter is:
4 + 5 + 6 = 15 cm.
So perimeter always tells you how much “border” a shape has.
What Is Area?
The area is the amount of space a shape covers on the inside. You measure it in square units—like square centimeters (cm²), square meters (m²), or square feet (ft²).
- For rectangles and squares, you multiply the length by the width.
- For triangles, it’s base × height ÷ 2.
- For circles, it’s π × radius × radius.
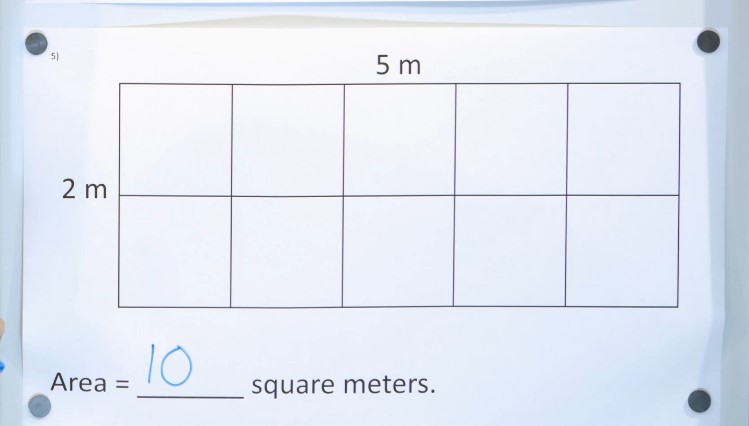
Example 1: Rectangles
A rectangle that is 10 meters long and 5 meters wide has an area of
10 × 5 = 50 square meters.
That means it covers 50 “squares” of 1 meter each. If you wanted to put tiles or carpet inside, you would need enough to cover 50 square meters.
Example 2: Triangles
If a triangle has a base of 6 cm and a height of 4 cm, its area is:
(6 × 4) ÷ 2 = 12 cm².
So area always tells you how much “room” is inside a shape.
| Feature | Area | Perimeter |
|---|---|---|
| What it measures | The amount of surface a shape covers inside its boundaries. | The total length of the outer boundary or edge of the shape. |
| Units | Always in square units (cm², m², ft², in²), because it counts “squares” that fit inside the shape. | Always in linear units (cm, m, ft, in), because it measures a single line that runs around the edge. |
| How to calculate | Use multiplication or formulas. Example: rectangle → length × width; triangle → base × height ÷ 2; circle → π × radius². | Add the lengths of all the sides. Example: rectangle → (length + width) × 2; triangle → side1 + side2 + side3; circle → 2 × π × radius. |
| Example (rectangle) | A rectangle with sides 10 m and 5 m has an area of 10 × 5 = 50 m². | The same rectangle has a perimeter of 10 + 5 + 10 + 5 = 30 m. |
| Real-life use | Used when you want to cover, fill, or paint something. Example: how much carpet covers a floor, how much paint covers a wall, how much grass covers a garden. | Used when you want to outline, enclose, or measure distance. Example: how much fence goes around a yard, how long the border of a frame is, or how far around a track someone runs. |
Why the Difference Matters in Real Life
Understanding the difference between area and perimeter is not just a math exercise—it’s something that shows up in everyday life, construction, sports, farming, and even art.
Building a fence or wall:
If you want to put a fence around your backyard, the perimeter tells you exactly how many meters of fencing to buy. If your yard is 30 meters around, that’s how much fence you need. But if you bought fencing based on the area, you would end up with way too much or too little, because area has nothing to do with the length of the boundary.
Laying carpet, tiles, or flooring:
When you need to cover a floor with carpet or tile, the area is the key. A room that is 5 meters long and 4 meters wide has an area of 20 m². That tells you how much carpet or how many tiles you must buy. The perimeter would only tell you how long the walls are—not useful for this job.
Painting walls or ceilings:

Paint covers surfaces, so you must measure the area. If one wall in your room is 3 meters high and 4 meters wide, its area is 12 m². If each can of paint covers 10 m², you know you need more than one can for that wall. The perimeter wouldn’t tell you this at all—it only measures the border of the wall.
Sports and running tracks:
Athletes measure their distance by perimeter. A 400-meter running track is defined by the perimeter of the oval. Runners care about how far it is around the track, not how much grass is in the middle. But for the groundskeeper, area matters too—because they need to know how much grass to cut inside the track.
Gardens and farming:
Farmers care about both. The area of their fields tells them how many crops they can plant and how much seed or fertilizer to buy. The perimeter tells them how much fencing or irrigation piping is needed around the edge. Without both, planning would be incomplete.
Everyday objects:
Even small tasks use these ideas. If you want to frame a family photo, you measure the perimeter to know the border length of the frame. If you want to laminate the same photo, you need to know the area to know how much plastic sheet will cover it.
Bottom Line
Perimeter = boundary distance. Area = inside space.
You need a perimeter when you measure around. You need an area when you measure inside. Knowing when to use each one saves time, money, and mistakes—whether you’re building something, covering a surface, or just trying to understand the world around you.
Related Posts:
- How the Environment Shapes Brain Growth Between Ages…
- Factors And Multiples For Kids: Simple Rules And Games
- Who Invented Math: History, Facts and Table of Numerals
- 8 Fun Activities to Practice Fractions and Mixed…
- What Are BODMAS, BIDMAS, and PEMDAS? A Simple Explanation
- What is a Point in Geometry? Definition and Examples