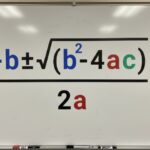Share Post:
Kids love talking about big numbers. A million. A billion. A googol with its string of zeros that feels like it could wrap around the block. Then someone whispers a word that feels almost magical: infinity.
Suddenly, you are in a world where numbers never run out, where you can keep counting and still never finish. But what is infinity really, and how do mathematicians use it?
Let’s take a walk through the idea, with puzzles, stories, and examples that even grown-ups find fascinating.
Table of Contents
ToggleKey Points
The Big Idea in One Sentence
Infinity simply means “without end.” If you can keep going and there is no last step, you are walking toward infinity. Think of the counting numbers: 1, 2, 3, 4, and so on. You never stop.
That never-ending pattern is where infinity lives. It is not a regular number you can put in a calculator. Instead, it is a way of describing endless processes.
Meet the ∞ Symbol
Chances are, you have seen the sideways figure eight. That is the symbol for infinity, written as ∞. It was first popularized in 1655 by the English mathematician John Wallis.
The symbol caught on because it looks like a loop with no start or finish. Kids often say it looks like a racetrack that never ends, which is not a bad way to think about it.
Infinity Is a Direction, Not a Destination

Picture a number line stretching to the right: 1, 2, 3, 4, 5… and further. You never land on a final step called infinity. You just keep moving.
That’s why mathematicians talk about “limits at infinity” rather than plugging infinity in as if it were a number. For example, in calculus, we ask questions like “What happens to f(x) as x grows without bound?”
Infinity is more like a direction you travel in than a place you can stop.
Infinity Is Not a Normal Number
Infinity does not play by the rules of ordinary arithmetic. Kids love to ask “What’s infinity plus one?” or “What happens if you double infinity?”
Mathematicians have answers that keep the idea sharp:
| Expression | What Mathematicians Say | Why It Makes Sense for Kids |
| ∞ + 1 | Still ∞ | If you already have something endless, adding one does not change that. |
| ∞ × 2 | Still ∞ | Doubling forever is still forever. |
| ∞ − ∞ | Undefined | Taking infinity away from infinity depends on how you built those infinities. No single answer works. |
| ∞ ÷ ∞ | Indeterminate | Sometimes it behaves like a number, sometimes not. It depends on the problem. |
In calculus, expressions like ∞ − ∞ and ∞ ÷ ∞ are called indeterminate forms, because the value depends on the exact situation.
That is why mathematicians treat infinity as a concept, not a standard number.
Two Kinds of “Forever” – Countable and Uncountable
Here is one of the most surprising discoveries in math: some infinities are bigger than others.
Countable Infinity
“Countable” means you can list items using 1, 2, 3, 4, … without missing any.
- The counting numbers themselves are countably infinite.
- The even numbers are also countably infinite. Pair them as 1↔2, 2↔4, 3↔6, and so on. Even though there are fewer even in everyday thought, there is a perfect one-to-one matching with all the counting numbers.
- Fractions are also countably infinite. By arranging them in a clever grid, you can eventually reach every one.
Uncountable Infinity
Then comes the mind-stretching part. The real numbers between 0 and 1 form a larger infinity. No matter how you try to list them, you will always miss some.
In the late 1800s, Georg Cantor showed this with his diagonal argument: by changing the digits in a list one by one, he could always create a brand-new number not on the list.
So there are different sizes of forever. Countable infinities can be matched with the counting numbers. Uncountable infinities, like the numbers on a line segment, are bigger.
Handy Comparison Table
| Type of Infinity | What It Includes | Can You List Them 1, 2, 3, …? | Example Idea |
| Countable | Whole numbers, integers, fractions | Yes | A hotel with rooms numbered 1, 2, 3, … |
| Uncountable | Real numbers on a line (even between 0 and 1) | No | Any decimal list will miss infinitely many numbers |
The Most Famous Story (Hilbert’s Hotel)
@zackdfilms92Hilbert’s Infinite Hotel 🤔 (explained)♬ original sound – Zack D. Films
Imagine a hotel with infinitely many rooms, all full. A new guest shows up. No room, right? Not if you are clever. Ask each guest in room n to move to room n+1.
Suddenly, room 1 is free. Now imagine a bus with infinitely many new guests arrives. You can still fit them in. Ask each guest in room n to move to room 2n.
That leaves every odd-numbered room open for the new guests. This playful thought experiment, created by David Hilbert, shows why infinity is not like ordinary numbers.
It has room for surprises.
Infinity in Geometry
Infinity is not just for numbers. A line segment, no matter how tiny, contains infinitely many points. Between any two points lies another. And between those, another.
That pattern never ends. The ancient Greeks, without the symbol ∞, still touched on the idea. They used the method of exhaustion to find areas and volumes, zooming in endlessly to get an exact result.
Infinity in Calculus
Calculus gives us practical tools for infinity. Instead of plugging infinity into a formula, mathematicians ask questions about behavior:
For example, the function 1/x gets closer and closer to 0 as x grows. We say the limit is 0 as x approaches infinity.
The function never actually reaches 0, but it gets as close as you like. That’s infinity at work in school math.
What Infinity Is Not
- Not the biggest number. Add one to any number and you have a new one. The game never ends.
- Not a place on the number line. Infinity is about continuing without stopping, not a final destination.
- Not guaranteed in physics. Whether the universe is infinite is still debated. Mathematics handles infinity neatly, but science may give different answers.
Quick Kid-Friendly Puzzles

Here are a few puzzles that bring infinity to life:
1. The Never-Ending Count
Start at any number and keep adding 1. Can you ever stop? Why not?
2. Even Numbers Are “As Many” As All Numbers
Pair 1↔2, 2↔4, 3↔6. Did you miss any? That shows equal “size” of infinity.
3. Fraction Zoom
Start at 1. Take half, then half again, then half again. You never reach 0, but you get closer forever.
4. Hilbert’s Mini-Hotel With Blocks
Label cups 1 to 10, then extend the idea. Practice shifting each one up by one to make space.
5. Diagonal Detectives
Try listing decimals between 0 and 1. Then change each digit diagonally to make a new number. Surprise: it is not on your list.
A Bit of History Kids Enjoy
Priest John Wallis was the first mathematician to introduce the symbol ∞ with its mathematical meaning of infinity in 1655 pic.twitter.com/DvXwPcCiq8
— Fermat’s Library (@fermatslibrary) August 16, 2017
- John Wallis made the infinity symbol popular in 1655.
- Georg Cantor proved that some infinities are larger than others.
- David Hilbert shared the hotel story in the early 1900s.
These names remind us that infinity is not just a child’s imagination. It has a history built by real mathematicians.
Classroom Language Tips for Parents and Teachers
Infinity vs. Very Large Number
| Question | Very Large Number | Infinity |
| Can you finish counting to it? | Yes, if you had time | No, there is no last step |
| Can you write it with digits? | Yes | No |
| Is it a place on the number line? | Yes | No, it is a direction |
| Do arithmetic rules apply? | Yes | Not in the usual way |
Summary
With these ideas, children can see infinity in counting, in shapes, and in school math. They will not only spot infinity, they will know how to talk about it with confidence.
Related Posts: