Share Post:
Absolute value tends to appear in calculus at the exact moment when a problem stops caring about direction and starts caring about size.
It shows up in distance, in total error, in total variation, in real physical measurement, and in many exam questions that quietly test whether you can separate net change from total accumulation.
A usual definite integral can subtract area when a curve dips below the horizontal axis. An absolute value integral refuses to subtract.
Every piece of area gets counted as area. Nothing disappears. That small change in notation completely changes what the number at the end actually represents.
The goal here is simple. Build comfort with what an integral of an absolute value means, how to compute it, and why it matters.
Table of Contents
ToggleWhy Absolute Value Appears Inside Integrals
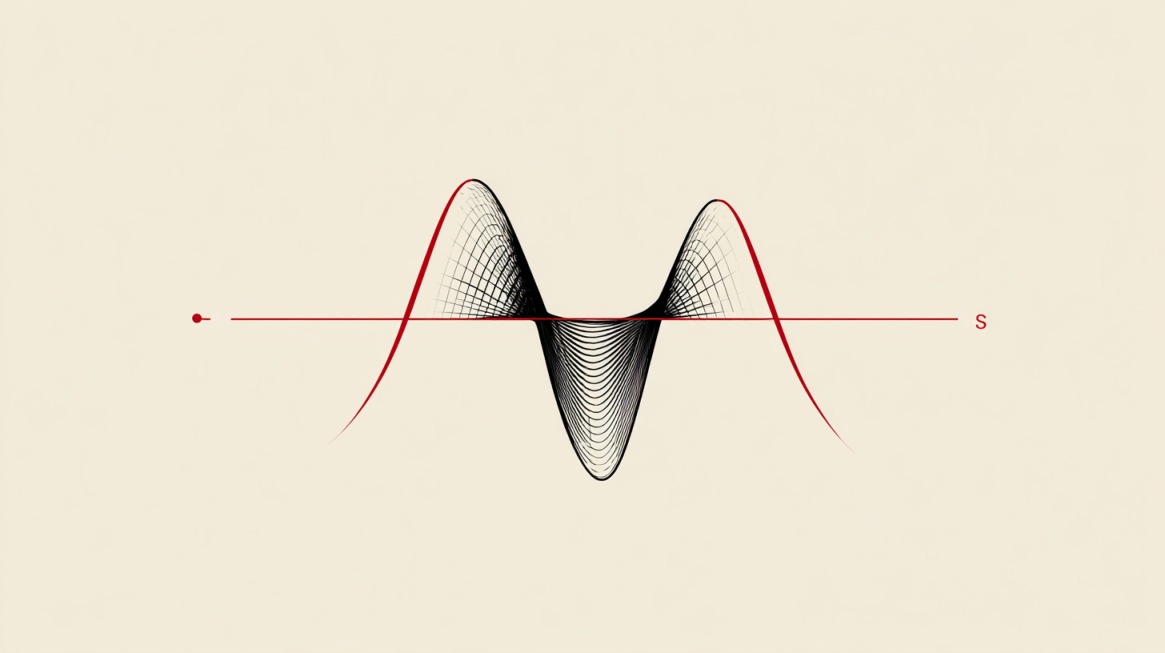
An ordinary definite integral counts the signed change. Parts of a graph above the axis add to the total. Parts below subtract from the total. That behavior works perfectly for quantities like displacement, profit minus loss, or net change.
Real measurements often need a different type of count.
- Total geometric area between a curve and the axis.
- Total distance traveled from a velocity function.
- Total accumulated error or deviation.
- Total variation in a signal or model.
In each case, negative values would damage the meaning of the result. Area cannot be negative. Distance cannot be negative. Error size cannot be negative. The bars fix that problem.
OpenStax phrases it directly. A standard integral produces a net signed area. The total area between a curve and the axis is computed by integrating the absolute value.
Net Signed Area Vs Total Area
A definite integral written in standard form,
∫ₐᵇ f(x) dx,
computes net signed area. Area above the axis contributes positive values. Area below contributes negative values.
A total area version replaces the integrand with its absolute value,
∫ₐᵇ |f(x)| dx.
That change forces every region to contribute positively. Nothing cancels out.
One can think of the bars as telling the integral to treat every vertical slice as having height equal to the magnitude of the function value.
Distance Vs Displacement In Motion
Velocity problems provide the cleanest physical meaning for absolute value integrals.
Let v(t) represent velocity.
Displacement over a time interval [a, b] is given by
∫ₐᵇ v(t) dt.
That value can be negative if motion leans backward more than forward.
Total distance traveled over the same time interval is
∫ₐᵇ |v(t)| dt.
Velocity can change sign. Distance cannot. Mathematics LibreTexts walks through this exact reasoning in motion examples.
How To Remove The Absolute Value
The key technique is never mysterious. Absolute value is defined piecewise.
|u| = u if u ≥ 0
|u| = −u if u < 0
A calculus text does not “anti-differentiate an absolute value.” One finds where the inside becomes zero, splits the interval, then integrates without bars.
Paul’s Online Notes emphasizes this as the standard workflow.
Step-by-Step Method For Definite Integrals

When given an integral of the form
∫ₐᵇ |g(x)| dx,
- Solve g(x) = 0.
- Keep only the solutions that lie in the interval [a, b].
- Determine the sign of g(x) on each resulting sub-interval.
- Rewrite |g(x)| as either g(x) or −g(x) on each sub-interval.
- Split the integral at the sign change points and evaluate each piece.
Interval splitting is justified by standard definite integral properties listed in Lumen Learning calculus notes and other mainstream texts.
Worked Examples
Example 1: Linear Expression
∫₀³ |3t − 5| dt
Step 1. Solve 3t − 5 = 0.
t = 5/3.
That value lies inside [0, 3].
Step 2. Determine the sign.
For t < 5/3, 3t − 5 < 0.
For t > 5/3, 3t − 5 > 0.
Rewrite:
|3t − 5| = 5 − 3t on [0, 5/3] |3t − 5| = 3t − 5 on [5/3, 3]
Step 3. Split the integral.
∫₀³ |3t − 5| dt = ∫₀^(5/3) (5 − 3t) dt + ∫_(5/3)³ (3t − 5) dt
Each piece now integrates normally.
Example 2: Quadratic With Two Zeros
∫₋₁² |x² − 1| dx
Step 1. Solve x² − 1 = 0.
x = −1, x = 1.
Both fall inside the interval, with −1 on the boundary.
Step 2. Sign behavior.
Between −1 and 1, x² − 1 ≤ 0.
For x ≥ 1, x² − 1 ≥ 0.
Rewrite:
|x² − 1| = 1 − x² on [−1, 1] |x² − 1| = x² − 1 on [1, 2]
Split:
∫₋₁² |x² − 1| dx = ∫₋₁¹ (1 − x²) dx + ∫₁² (x² − 1) dx
Example 3: Distance From Velocity
v(t) = 3t − 5 for t in [0, 3].
Net displacement is
∫₀³ (3t − 5) dt.
Total distance traveled is
∫₀³ |v(t)| dt.
Find the sign change:
3t − 5 = 0 → t = 5/3.
Split:
∫₀³ |v(t)| dt = ∫₀^(5/3) (5 − 3t) dt + ∫_(5/3)³ (3t − 5) dt
LibreTexts demonstrates this exact setup and reports an evaluated result for the same configuration.
Example 4: Trigonometric Case
∫₀^(2π) |sin x| dx
Key sign points:
sin x = 0 at x = 0, π, 2π.
On [0, π], sin x ≥ 0.
On [π, 2π], sin x ≤ 0.
Rewrite:
|sin x| = sin x on [0, π] |sin x| = −sin x on [π, 2π]
Split:
∫₀^(2π) |sin x| dx = ∫₀^π sin x dx + ∫_π^(2π) (−sin x) dx
Indefinite Integrals With Absolute Value

Indefinite integrals require piecewise antiderivatives.
Example 5: ∫ |x − 2| dx
x = 2.
Rewrite:
For x < 2, |x − 2| = 2 − x.
For x ≥ 2, |x − 2| = x − 2.
Integrate:
For x < 2:
∫ (2 − x) dx = 2x − x²/2 + C₁
For x ≥ 2:
∫ (x − 2) dx = x²/2 − 2x + C₂
Many courses choose constants so that both expressions match at x = 2.
A Compact Identity You May See
A frequently used formula is
∫ |x − a| dx = (1/2)(x − a)|x − a| + C
Differentiation verifies the result piecewise. The interval-splitting approach remains the most dependable method for definite integrals.
A Practical Checklist
Common mistakes repeat every semester.
- Forgetting to split at every sign change.
- Splitting at an incorrect point by solving the wrong equation.
- Treating |g(x)| as g(x) without checking the sign.
- Mixing displacement with distance.
- Dropping bars in an indefinite integral without stating cases.
LibreTexts explicitly stresses the distance versus displacement distinction in motion problems.
Why ∫|f| Can Exceed |∫f|
Absolute value removes cancellation.
From the number inequality
−|y| ≤ y ≤ |y|,
and the comparison property of integrals listed in the Lumen Learning calculus notes,
one obtains:
−∫ₐᵇ |f(x)| dx ≤ ∫ₐᵇ f(x) dx ≤ ∫ₐᵇ |f(x)| dx
which implies
|∫ₐᵇ f(x) dx| ≤ ∫ₐᵇ |f(x)| dx
Net effect never exceeds total accumulated magnitude.
Quick Reference Table
| Integrand | What To Do | Split Points |
| x − a | Solve x − a = 0 | x = a |
| ax + b | Solve ax + b = 0 | x = −b/a |
| x² − c² | Solve x² − c² = 0 | x = ±c |
| sin x | Use sine sign pattern | multiples of π |
| v(t) | Use velocity sign | where v(t) = 0 |
The same split-and-rewrite technique applies in every row.
Why Learners See This Topic Often
Absolute value integrals appear regularly in early calculus and in AP Calculus motion applications.
College Board data show 285,891 AP Calculus AB test takers in 2025, with a reported mean score of 2.89. That number reflects how central such material remains in mainstream assessment.
Final Notes
Absolute value inside an integral removes cancellation and forces every contribution to count. That single change converts displacement into distance, net area into total area, and signed deviation into accumulated magnitude.
The computation always follows the same reliable path. Find where the inside changes sign. Split the interval. Integrate without bars.
No shortcuts beat that method.
Related Posts:
- Prime Numbers Explained For Kids With Easy Examples…
- Greatest Common Factor Explained with Visual Examples
- What is a Point in Geometry? Definition and Examples
- What Are the Types of Polynomials? Definitions and Examples
- Complete Guide to Teaching Math with Base 10 Blocks…
- Natural Numbers - Definition, Properties, and Examples