Share Post:
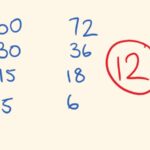
The greatest common factor GCF is the largest whole number that divides two or more integers without leaving a remainder. If you take 24 and 36, the GCF is 12 because 12 is the biggest number that divides both evenly.
This idea sits at the core of simplifying fractions, comparing quantities, scaling measurements, and structuring many basic algebraic operations taught worldwide in elementary and middle school mathematics.
A factor is any integer that divides another integer exactly. For the number 18, the complete factor set is 1, 2, 3, 6, 9, and 18. Every whole number has at least two factors: 1 and itself.
Composite numbers have more than two, while prime numbers have exactly two. The idea of a common factor simply refers to overlap between factor sets of two or more numbers.
The term โgreatestโ in GCF is literal. Among all shared factors, only the largest one qualifies. Smaller shared factors still matter, but they are not sufficient when a problem explicitly asks for the greatest.
Listing Factors Method
The most direct method for finding the GCF is listing all factors of each number and identifying the largest shared value. While this approach is slow for large numbers, it provides clarity and is commonly introduced first in classrooms.
Factor Listing Example
Number
All Factors
24
1, 2, 3, 4, 6, 8, 12, 24
36
1, 2, 3, 4, 6, 9, 12, 18, 36
The common factors here are 1, 2, 3, 4, 6, and 12. The largest of these is 12, so the GCF is 12.
This method is transparent and easy to verify, but it becomes inefficient when numbers exceed two digits or when many numbers are involved.
Prime Factorization Method
Prime factorization breaks each number into its prime building blocks. This approach is faster, scalable, and preferred in formal mathematics instruction.
For example:
- 24 = 2 ร 2 ร 2 ร 3
- 36 = 2 ร 2 ร 3 ร 3
To find the GCF, identify only the prime factors that appear in both factorizations, using the lowest exponent shared.
Prime Factor Comparison
Prime Factor
24
36
Used for GCF
2
2ยณ
2ยฒ
2ยฒ
3
3ยน
3ยฒ
3ยน
Multiplying the shared factors gives 2ยฒ ร 3 = 4 ร 3 = 12.
This method forms the foundation for algebraic factoring and fraction reduction and is emphasized in international math standards such as Common Core and Cambridge curricula.
Visual Arrays and Area Models
A visual way to understand GCF is through rectangular arrays. If you arrange objects into equal rows and columns, the GCF represents the largest rectangle size that works for all quantities.
Imagine 24 and 36 identical tiles. Both can form rectangles with 12 tiles per side:
- 24 = 12 ร 2
- 36 = 12 ร 3
No larger shared side length is possible. This makes 12 the greatest common factor.
Educators rely on this model because it connects numerical abstraction to spatial reasoning, which research in math cognition has shown improves long-term retention.
Using the GCF to Simplify Fractions
View this post on Instagram
The most common real-world use of the GCF is fraction simplification. A fraction is in its simplest form when the numerator and denominator share no common factor other than 1.
Fraction Simplification Using GCF
Original Fraction
GCF
Simplified Form
24/36
12
2/3
18/30
6
3/5
45/60
15
3/4
Dividing both numerator and denominator by the GCF preserves the value of the fraction while reducing complexity. This principle underpins ratio analysis, probability calculations, and unit conversions in science and engineering.
GCF Versus LCM
GCF is often taught alongside LCM least common multiple, but they answer opposite questions. GCF looks for the largest shared divisor, while LCM finds the smallest shared multiple.
GCF vs LCM Comparison
Aspect
GCF
LCM
Purpose
Largest shared divisor
Smallest shared multiple
Typical use
Simplifying, grouping
Scheduling, alignment
Example for 12 and 18
6
36
Understanding both allows students to solve a wider class of number problems, particularly in fraction operations and word problems involving cycles or repetition.
GCF With More Than Two Numbers
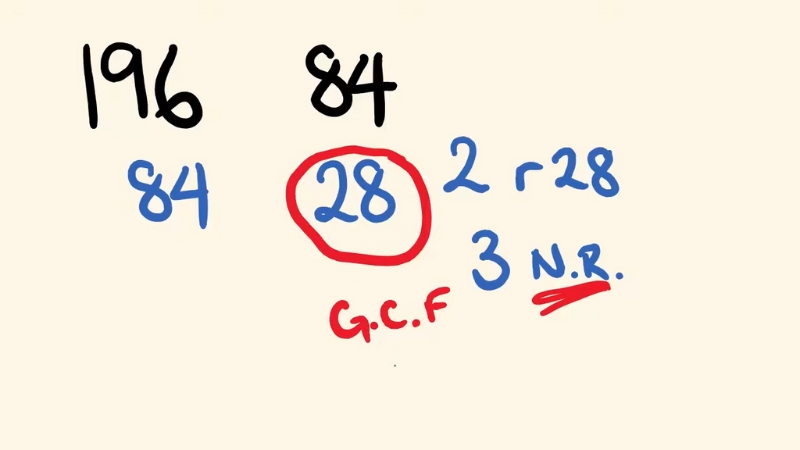
The concept extends naturally to three or more numbers. The GCF must divide all numbers involved.
Example: 18, 24, and 30
- Prime factorizations:
- 18 = 2 ร 3ยฒ
- 24 = 2ยณ ร 3
- 30 = 2 ร 3 ร 5
Shared primes are 2ยน and 3ยน. The GCF is 2 ร 3 = 6.
As the number of values increases, the GCF often decreases. This pattern is relevant in data normalization and resource allocation problems.
GCF in Algebraic Expressions
In algebra, GCF applies to variables as well as numbers. Consider:
12xยฒy + 18xyยฒ
The numeric GCF of 12 and 18 is 6. The shared variables are xยน and yยน. Factoring out the GCF gives:
6xy(2x + 3y)
This step is essential in polynomial factoring, equation solving, and simplifying rational expressions. It also reduces computational errors by keeping expressions compact.
Why the Greatest Common Factor Matters
@impactmath19 Replying to @MADISON hope this helps:) #impactmath19 #factor #math #factoroutgcf #factoring #factoringbinomials โฌ Pressure – Instrumental – KPH
The GCF is not a decorative concept. It determines how efficiently quantities can be grouped, reduced, or compared.
It underlies fraction arithmetic, ratio reasoning, polynomial factoring, and even computational optimizations in computer science, where common divisors reduce processing overhead.
From elementary classrooms to algebraic modeling, the GCF serves as a structural tool. When it is understood visually and numerically, it becomes intuitive rather than procedural.
